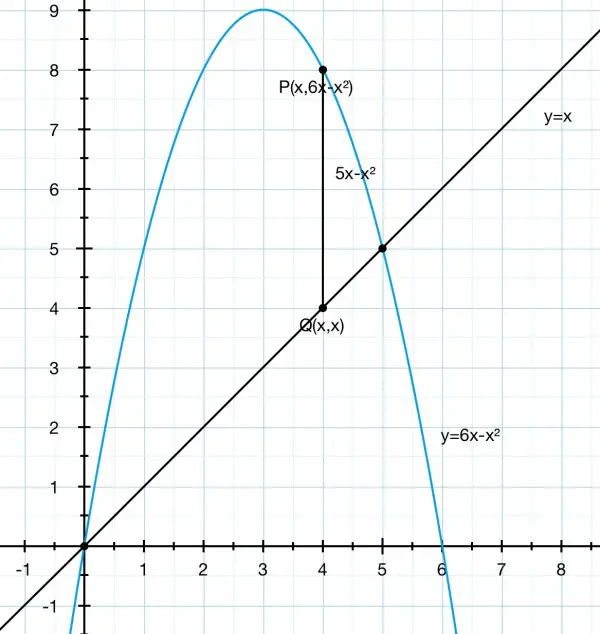
(a) The picture shows the given curve and line. The line PQ shows the height of a cylinder where P is a point on the curve. The cylinder is the result of rotating the line PQ about the y-axis as the axis of rotation (x=0). The line and curve intersect when x=6x-x^2, that is, x(5-x)=0 at x=0 and 5. The cylinder is hollow with an infinitesimally thin wall, thickness dx. The radius of the cylinder is x, the height of the cylinder is 5x-x^2 as can be seen by the geometry, and the area of this cylindrical shell is found by "rolling out" the cylinder into a rectangular lamina. So the length of the rectangle is 2πx, the circumference of the cylinder, and the height 5x-x^2, making the area 2πx^2(5-x). The volume of the cylinder is the area multiplied by the thickness dx: 2πx^2(5-x)dx. The sum of the volumes of the cylindrical shells gives us the volume of rotation of the shape bounded by the line and curve. This sum is ∫(2πx^2(5-x)dx) between the limits x=0 to 5. The integral evaluates to 2π(5x^3/3-x^4/4) and, applying the limits: 2π(625/3-625/4)=625π/6=327.25 cu units approx.
(b)
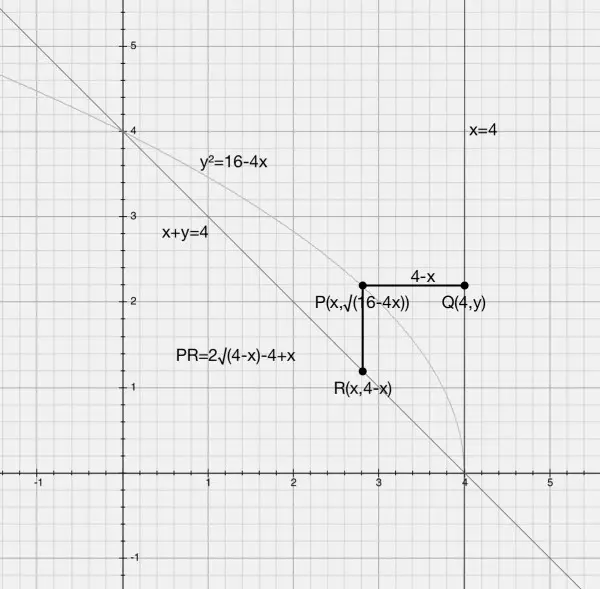
This time we have a cylinder radius 4-x and height PR=2√(4-x)-4+x. The volume of the cylindrical shell is 2π(4-x)(2√(4-x)-4+x)dx and the integral ∫(2π(4-x)(2√(4-x)-4+x)dx). Since y=4-x we can replace 4-x with y and dx by -dy. The integral becomes -2π∫(y(2√y-y)dy). Since x=4-y and x=(16-y^2)/4 we can write 4-y=(16-y^2)/4 and solve for y. 16-4y=16-y^2 so y(4-y)=0 and y=0 and 4 as evidenced in the picture. The limits are 4≥y≥0. The minus on the integral is changed to plus if we reverse the limits for y.
So we need to evaluate the definite integral: 2π∫((2y^(3/2)-y^2)dy)=2π[(4/5)z^(5/2)-z^3/3] for 0≤y≤4. This evaluates to 2π(128/5-64/3)=128π/15=26.81 cu units approx.
(c)
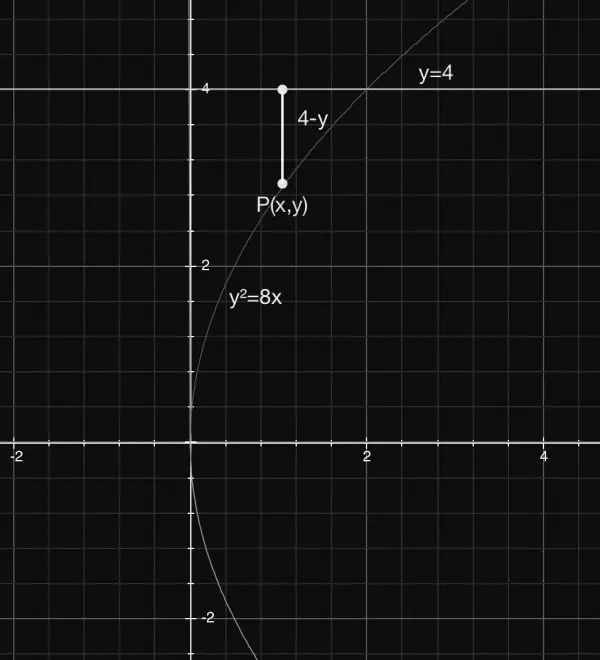
The intersection point between the parabola and line y=4 is given by 16=8x, so x=2 and y=4: (2,4). The parabola meets the y-axis (x=0) at the origin (0,0). For a point P(x,y) on the parabola 4-y is the radius of a disc of thickness dx and therefore the volume of the disc is π(4-y)^2dx=π(16-8y+y^2)dx. Since y^2=8x we can evaluate the integral π∫((16-16√(2x)+8x)dx) for 0≤x≤2 to find the volume of revolution around the line y=4. This evaluates to 8π[2x-4√2x^(3/2)/3+4x^2] for 0≤x≤2=8π(4-16/3+16)=352π/3=368.61 cu units.