4. Find the volume of the solid generated by revolving about the line x=3 the region x=3 the region bounded by the line, the x-axis and the graph of y=9x-12x⁴

Question

Show complete solution

Answer 1

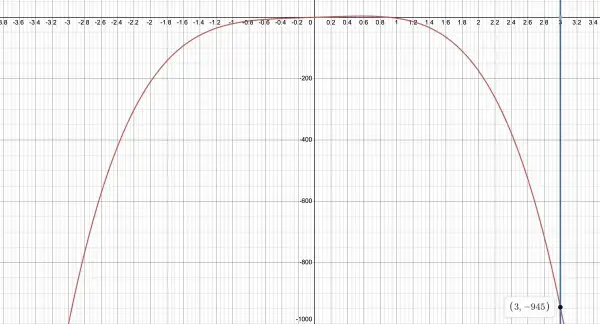
The region specified I understand to be shown above below the x-axis between the red curve y=9x-12x⁴ and blue line x=3, which meet at (3,-945), where 9×3-12×81=-945. This region is to be rotated around the blue line as axis of rotation. The distance between any point P(x,y) on the curve and the line forms the radius of a circle and a disc is created by the rotating point. The area of the disc is π(3-x)². If the disc has a thickness dy, its volume is π(3-x)²dy so the volume of the solid created by many stacked discs=_-945∫⁰π(3-x)²dy. Since y=9x-12x⁴, dy can be replaced by (9-48x³)dx, and the limits changed. When y=0, 9x-12x⁴=0=3x(3-4x³), so x=0 or ∛¾. The latter is the actual low limit for x while x=3 is the high limit. Because of the scale of the graph it's not easy to see the low limit.

We can now evaluate the integral:

π_∛¾∫³(3-x)²(9-48x³)dx=

π_∛¾∫³(9-6x+x²)(9-48x³)dx=

π_∛¾∫³(81-54x+9x²-432x³+288x⁴-48x⁵)dx=

π[81x-27x²+3x³-108x⁴+288x⁵/5-8x⁶]_∛¾³=

π[(243-243+81-8748+69984/5-5832)-(81∛¾-27(¾^⅔)+9/4-108(¾^4/3)+288(¾^5/3)-9/2)=

-π(502.2+11.1228)=-513.323π =-1612.65 cubic units approx.

This volume lies below the x-axis, hence the negative sign, so the actual volume of this "pinnacle" is about 1612.65 cubic units.

(A cone with base radius 2 and height 945 has a volume of ⅓(2²)×945π=1260π=3958.41 cubic units. Since the cone encloses the pinnacle, the volume of the cone should exceed the volume of the pinnacle---which it clearly does.)