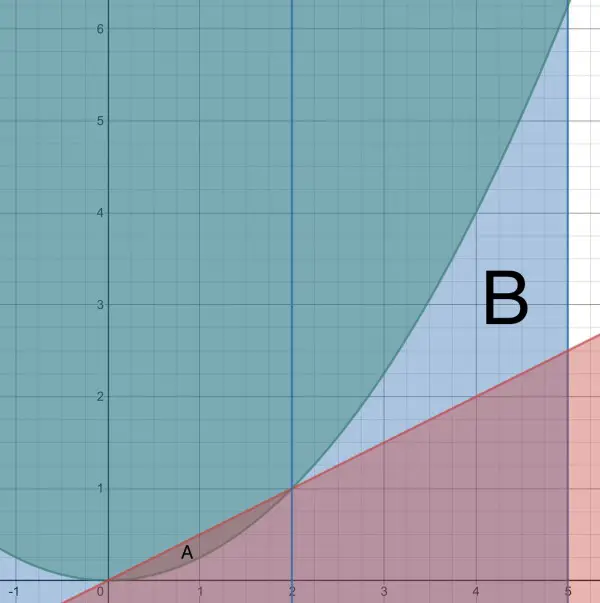
Split the area into two regions A and B.
REGION A
A is the region above the curve and below the straight line. It is bound on the left by the point (0,0), the origin, and on the right by the point (2,1), because ¼x²=½x has the solution x=0 or 2. Consider a point x on the x-axis. Rotate the point around the y-axis and we get a circle with circumference 2πx. If we build a cylinder with the circle as a base, the height of the cylinder will be x/2. If the thickness of the cylindrical wall is dx, the volume of the cylinder will be (2πx)(x/2)dx=πx²dx. The volume of the triangular part of A is ∫πx²dx for x∈[0,2]=(πx³/3)[0,2]=8π/3 cubic units.
We can treat the area under the curve in the same way, but this time the height of the cylinder is x²/4, so the volume of the thin cylinder is (2πx)(x²/4)dx=(πx³/2)dx. The rotated volume is ∫(πx³/2)dx=(πx⁴/8)[0,2]=2π cubic units. So the volume of region Ais 8π/3-2π=⅔π cubic units.
We also get this answer if we integrate ∫(πx²-πx³/2)dx=π∫x²(1-x/2)dx for [0,2].
REGION B
B is the region below the curve and above the straight line, so we subtract the area between the red hypotenuse and the x-axis from the area under the curve.
This reverses the order for the integral we used for region A and changes the limits:
∫(πx³/2-πx²)dx for [2,5]=π(x⁴/8-x³/3)[2,5]=π(625/8-125/3-2+8/3)=297π/8. cubic units.
The total volume of revolution is ⅔π+297π/8=907π/24=118.73 cubic units approx.
This is an alternative solution using a different method. It confirms the result in the solution above using cylinders.
WASHER METHOD
In this method we have 3 regions. Region B is split into B1 and B2. The line y=5/2 divides B into B1 above the line and B2 below.
REGION A
The washer is the difference between the areas of two disks. The outer radius is 2√y (because x²=4y) and the inner radius is 2y (because y=x/2), so the difference in areas is π(4y-4y²), and if the thickness of the disk is dy, the volume of the disk is π(4y-4y²)dy, from which we get the integral ∫π(4y-4y²)dy. The limits for y are [0,1].
Volume of region A rotated is π(2y²-4y³/3)[0,1]=π(2-4/3)=⅔π as before.
REGION B
Region B2 is the y interval [1,5/2], because the border line x=5 intersects the red line at (5,5/2). The outer radius is 2y and the inner radius 2√y. The integral is π∫(4y²-4y)dy[1,5/2]=π(4y³/3-2y²)[1,5/2]=(25/3+2/3)π=9π.
Region B1 is bounded by the vertical x=5, so the outer radius is 5, a constant. The curve 4y=x² meets x=5 when y=25/4. So the limits of the next integration are [1,25/4]. The inner radius is 2√y so the integral is π∫(25-4y)dy for [1,25/4].
So the volume is π(25y-2y²)[5/2,25/4]=π(625/8-50)=225π/8.
The total volume for B is 9π+225π/8=297π/8.
Region A+regionB=297π/8+2π/3=907π/24=118.73 cubic units approx. This is the same as by the first method.