Find the volume of the solid whose base is the region bounded by y=x^7, y=1,

Question

and the y-axis and whose cross-sections perpendicular to the x axis are semicircles.

Answer 1

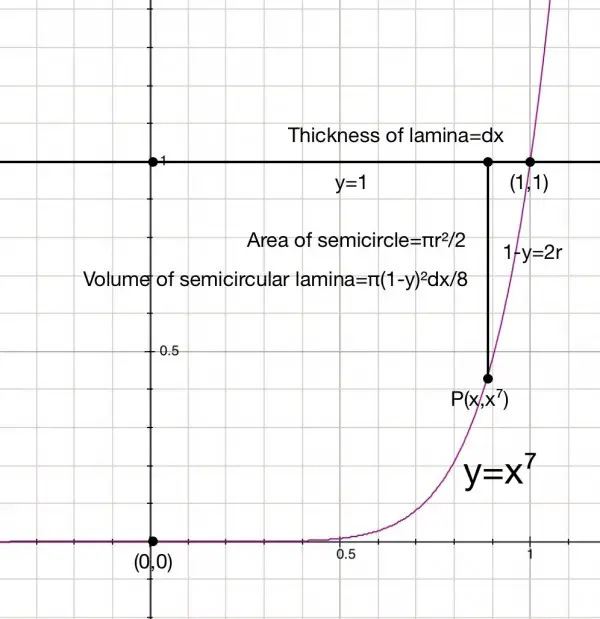
The radius of each semicircle is (1-y)/2 which equals (1-x^7)/2. The area of such a semicircle is π((1-y)/2)^2/2=π(1-y)^2/8. If the semicircle has a thickness dx the volume of the semicircular section is π(1-y)^2dx/8. When y=1, x=1, and (0,0) is the starting point. The volume of the first semicircular slice is when y=0, making the volume πdx/8, and the volume of the last semicircular slice is 0. So (π/8)∫((1-x^7)^2dx) for 0≤x≤1 gives us the volume.

Expanding this we have: (π/8)∫((1-2x^7+x^14)dx)=(π/8)[x-x^8/4+x^15/15] for 0≤x≤1.

This gives us (π/8)(1-1/4+1/15)=(π/480)(60-15+4)=49π/480=0.3207 approx.