Find the volume of the solid generated when the region enclosed by y=√x,x=9, and y=0 is revolved about the line x=9, and y=0 is revolved about the line x=9.
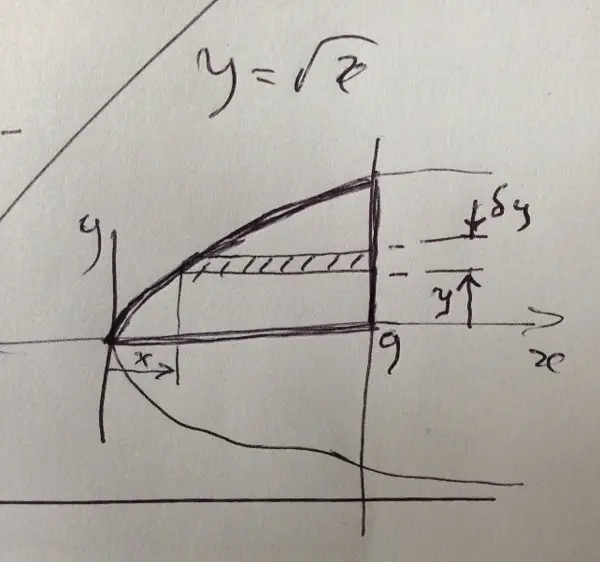
Consider the hatched area.
A volume of revolution (thin disc) can be generated by rotating the hatched area about the line x = 9.
The elemental volume of this disc would be
dV = pi.(9 - x)^2, dy
Integrating, to get the total volume,
V = pi * int[0 .. 3] (9 - x)^2 dy
substituting for x = y^2,
V = pi * int[0 .. 3] (9 - y^2)^2 dy
V = pi * int[0 .. 3] (81 - 18y^2 + y^4)^2 dy
V = pi * [81y - 6y^3 + (1/5)y^5] [ 0..3 ]
V = pi * {(243 - 162 + 48.6) - ( 0 )}
V = 129.6pi