The picture below illustrates the problem.
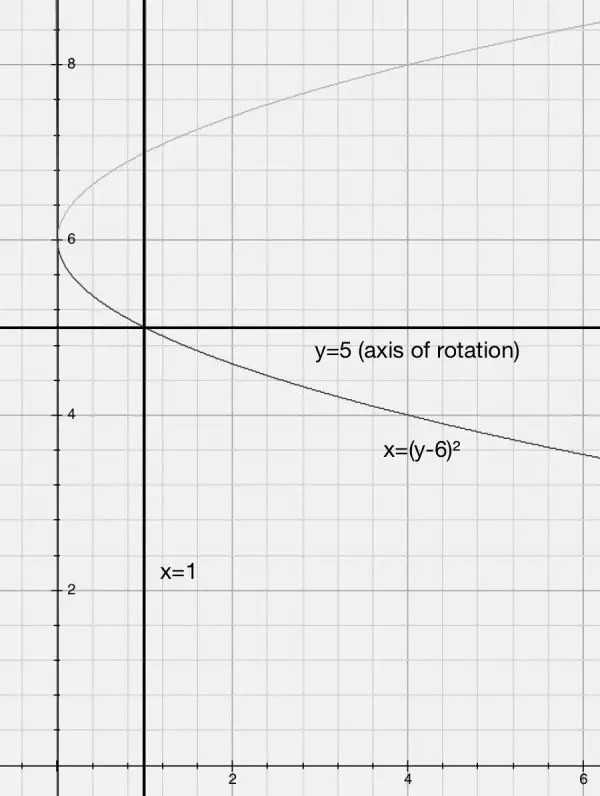
From this picture we can see that the tip of the sideways parabola is to be rotated around the axis y=5 that it is lying upon. When y=6, x=0 (vertex) and the part of the parabola we need is therefore between x=0 and 1.
Since x=(y-6)^2, then y=6±√x. This gives us two circles for each x value. The larger circle has a radius of 6+√x-5=1+√x and the smaller circle has a radius of 1-√x. The difference between the areas of these two circles gives the area of a "washer": π((1+√x)^2-(1-√x)^2)=π(1+√x-1+√x)(1+√x+1-√x)=4π√x. The volume of the washer is 4π√xdx for an infinitesimally thin washer, thickness dx. If we integrate 4π∫(√xdx)=4π[(2/3)x^(3/2)] for 0≤x≤1, we get 8π/3=8.3776 cu units = volume of revolution.
ALTERNATIVE APPROACH
x=(y-6)^2 so √x=y-6 and dx=2(y-6)dy. The volume of the washer is 4π(y-6)dx=8π∫((y-6)^2dy) = 8π∫((y^2-12y+36)dy). The limits are found through solving x=1=(y-6)^2 making the intersections (1,5) and (1,7). But when x=0, y=6, so the limits are 6≤y≤7 not 5≤y≤7.
Integrating: 8π[y^3/3-6y^2+36y] for 6≤y≤7=8π((7^3-6^3)/3-6(7^2-6^2)+36(7-6))=8π(127/3-78+36)=8π/3.
The same result applies if we take the limits 5≤y≤6=8π((6^3-5^3)/3-6(6^2-5^2)+36(6-5))=8π(91/3-66+36)=8π/3.
Had we used 5≤y≤7 we would have included the same volume twice, so the result would have been 16π/3.