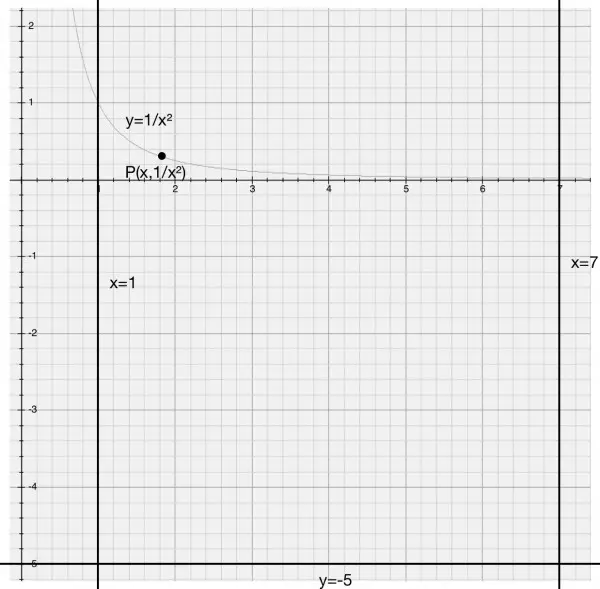
The point P(x,1/x^2) lies on the curve at a distance 5+1/x^2 from the axis of rotation, y=-5. When P rotates around y=-5, it describes a circle radius 5+1/x^2. All points on line y=0 (the x-axis) describe a circle radius 5 when similarly rotated. The area between the two circles is π((5+1/x^2)^2-25), which is the area of a "washer". If we add thickness dx to the washer we get the volume π((5+1/x^2)^2-25)dx. As x moves between x=1 and x=7 the washer gets narrower. The integral π∫((5+1/x^2)^2-25)dx) is the sum of all the infinitesimally thin washers for 1≤x≤7.
The integrand expands to (25+2/x^2+1/x^4-25)dx=(2x^-2+x^-4)dx and when we integrate this we get -π[2/x+1/(3x^3)] for 1≤x≤7, which evaluates to -π(2(1/7-1)+(1/3)(1/343-1))=π(12/7+114/343)=702π/343=6.43 cu units approx.