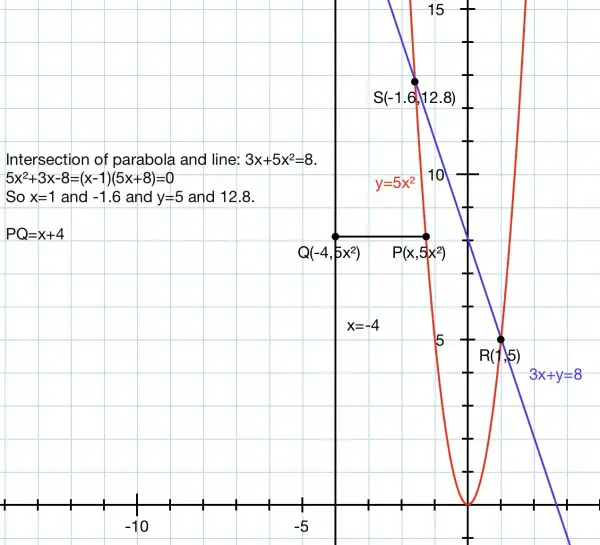
The picture shows the parabola and line and the axis of rotation.
We can split the volume into parts, starting with the tip of the parabola. This volume can be calculated by considering infinitesimally thin horizontal discs of radius x+4 and thickness dy, volume π(x+4)^2dy, between limits [-1 to 1]. Since y=5x^2, dy=10xdx. Thus we arrive at V=10π∫(x(x+4)^2dx) = 10π∫((x^3+8x^2+16x)dx) = 10π[x^4/4+8x^3/3+8x^2] for -1≤x≤1 = 10π(1/4-1/4+8/3-(-8/3)+8-8)=160π/3.
For the remaining part of the volume for -1.6≤x≤-1 we subtract the inner volume created by the parabola from the outer volume created by the straight line (frustum). Vi (inner volume)=10π[x^4/4+8x^3/3+8x^2] for -1.6≤x≤-1=10π(11.1957-5.5833)=56.124π=176.3187. Vo (outer volume)=π∫(x+4)^2dy. Since y=8-3x, dy=-3dx so Vo=-3π∫((x+4)^2dx)=-3π∫((x^2+8x+16)dx) for -1.6≤x≤1. Vo=-3π[x^3/3+4x^2+16x] for -1.6≤x≤1=111.176π. Vo-Vi=(111.176-56.124)π = 55.052π = 172.95 approx.
(The volume of a frustum (truncated cone) is (1/3)π(R^2H-r^2h) where R is the base radius and r the top radius, H is the height of the complete cone and h the height of its tip (which is removed). H=20-5=15 because the line meets x=-4 at y=20 (-12+y=8) and h=20-12.8=7.2. R=5 and r=-1.6-(-4)=2.4. So the volume of the frustum is (1/3)π(25*15-5.76*7.2)=13897π/125=111.176π=349.2697 approx. This is also the calculated value of Vo using calculus.)
Combining this with the volume of the tip we get (55.052+160/3)π=108.3853π=340.50 cu units approx.