The curve y=x² is a parabola. The y-axis forms the “spindle” around which the parabola is to be rotated to form the solid. The limits of x=1 and y=8 are a little ambiguous. But let’s start with the basic disk method. Simply rotating the parabola around the y-axis is equivalent to summing the volumes of horizontal disks of radius x and thickness dy, giving rise to the integral ∫πx²dy or π∫ydy because y=x². When x=1, y=1²=1, so we appear to have the definite integral between y=1 and y=8: π(y²/2)[1,8]=(π/2)(8²-1)=63π/2.
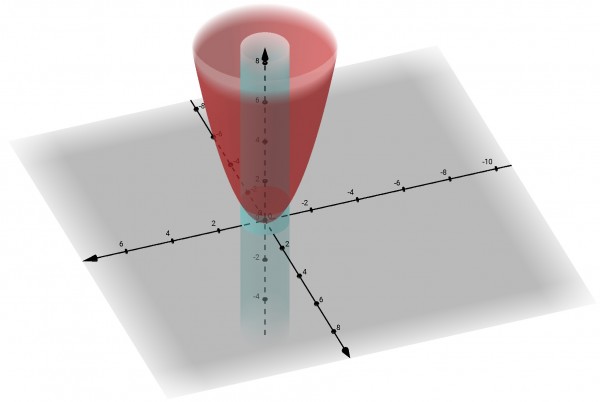
Above y=1 the cylinder is inside the paraboloid; below y=1 the paraboloid is inside the cylinder. The grey plane is the rotated x-axis. We are only dealing with volumes above this plane.
But if the limit x=1 is a boundary rather than a limit for the integral, x=1 is a cylinder intersecting the paraboloid. The question also mentions the x-axis. So another interpretation of the question is to calculate the volume of the solid created by subtracting the volume of the paraboloid between y=0 and y=1 from the volume of the cylinder of height 1 and radius 1, volume π cubic units. The volume of this part of the paraboloid is π(y²/2)[0,1]=π/2 cubic units. So the volume of this part is π-π/2=π/2 cubic units. To this we need to add the volume between the cylinder from y=1 to y=8, radius 1, and the parabola from y=1 to y=8. We know this volume to be 63π/2. The volume of the cylinder is π(8-1)(1)=7π. The difference between these volumes is 49π/2. Therefore the total volume would be π/2+49π/2=25π cubic units.