The line x=y bisects the enclosed area of the other curve x^4+y^2=12. The x coords of the points of intersection are given by x^4+x^2-12=0=(x^2+4)(x^2-3), so x=±sqrt(3).
The y coords are given by y=x, so the points are (sqrt(3),sqrt(3)) and (-sqrt(3),-sqrt(3)).
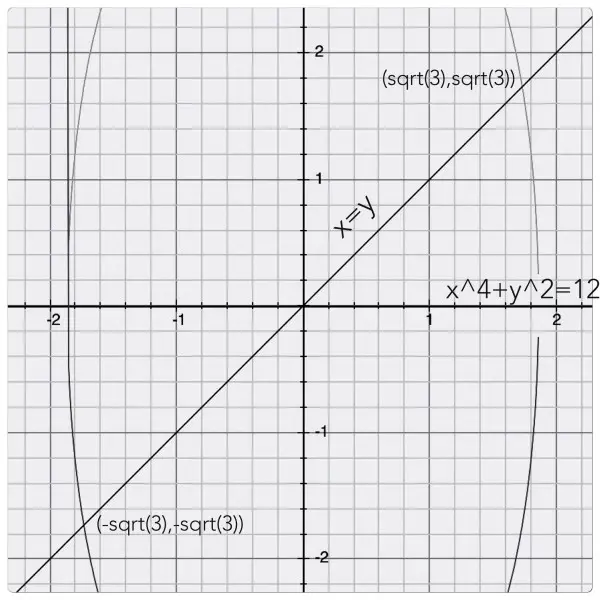
The picture shows how the area is bisected, so all we need to do is to find the area of the whole figure and halve it. But x^4+y^2=12 is symmetrical so to find the area of the whole figure, we just look at a quadrant and find its area, then we double the result to find the area enclosed by the line and the curve. When y=0 we have x intercept: x^4=12, so the area of a quadrant is integral of ydx between x=0 and x=12^(1/4), where y=sqrt(12-x^2) and the integrand is sqrt(12-x^2)dx.
Let x=sqrt(12)sin(z); dx=sqrt(12)cos(z)dz, so the integrand becomes:
sqrt(12-12sin^2(z))sqrt(12)cos(z)dz=12cos^2(z)dz.
cos(2z)=2cos^2(z)-1, so 2cos^2(z)=1+cos(2z) and 12cos^2(z)=6+6cos(2z).
But x=sqrt(12)sin(z), so if x=0, z=0 and if x=12^(1/4), sin(z)=12^(1/4)/12^(1/2)=12^(-1/4), z=sin^-1(12^(-1/4)).
sin(z)=12^(-1/4); cos(z)=sqrt(1-12^(-1/2)).
The result of integration is: 6z+3sin(2z) between the limits 0 and sin^-1(12^(-1/4)).
Plugging in values we get the area of a quadrant is 3.4033 + 2.7189 = 6.1222 approx., making half the area of the figure12.2443 approx. It doesn't matter that the line x=y splits the area obliquely, it is still half the area.