y=√x and y=x intersect at x=0 and x=1. The intersections enclose a figure (see graph below).
If this figure is made of material of uniform density ρ g/cm2 we can define the mass of any area A as ρA.
Consider the enclosed region to consist of narrow vertical rectangular strips of width dx.
The length of each strip is √x-x, so its area A=(√x-x)dx, and mass ρ(√x-x)dx.
The mass creates a moment of inertia about the y-axis=
mass times distance from the y-axis=(ρ(√x-x)dx)(x)=ρx(√x-x)dx.
The sum of all moments of inertia is 0∫1ρ(x3/2-x2)dx=ρ[⅖x5/2-⅓x3]01=ρ/15.
The total mass M of the enclosed area=0∫1ρ(√x-x)dx=ρ[⅔x3/2-x2/2]01=⅙ρ.
If the x-coordinate of the centroid is X, then MX is the moment about the y-axis that must counterbalance the total moment of inertia of the strips:
MX=ρ/15,
so X=(ρ/15)/(ρ/6)=6/15=⅖.
To find the y-coordinate we can consider horizontal rectangular strips of width dy. Since y=√x, y2=x.
The length of each strip is y-y2 (note that y2≤y in the interval [0,1]), so its mass is:
ρ(y-y2)dy.
M=⅙ρ, the same as before.
The mass creates a moment of inertia about the x-axis=ρy(y-y2)dy.
The sum of all moments of inertia is 0∫1ρ(y2-y3)dy=ρ[⅓y3-¼y4]01=ρ/12.
MY=ρ/12, Y=ρ/12/(⅙ρ)=½.
The centroid is at (X,Y)=(⅖,½).
ALTERNATIVE METHOD FOR FINDING Y
A more conventional approach to finding Y is to use the centres of mass of the vertical rectangular strips.
The length of each strip is √x-x, and the centre of mass of a rectangle is half its length=½(√x-x).
Its distance from the x-axis is x+½(√x-x)=½(√x+x).
Its moment about the x-axis is mass times distance from the x-axis:
(ρ(√x-x)dx)(½(√x+x))=½ρ(x-x2)dx.
The total of the moments= 0∫1½ρ(x-x2)dx=½ρ[½x2-⅓x3]01=½ρ(⅙)=ρ/12.
MY=ρ/12, Y=ρ/12/(⅙ρ)=½, which is the same value as before.
[A similar approach can be used to find X from horizontal strips. This time the sum of the moments is:
∫½ρ(y2-y4)dy=½ρ[⅓y3-⅕y5]01=½ρ(⅓-⅕)=½ρ(2/15)=ρ/15, as before.]
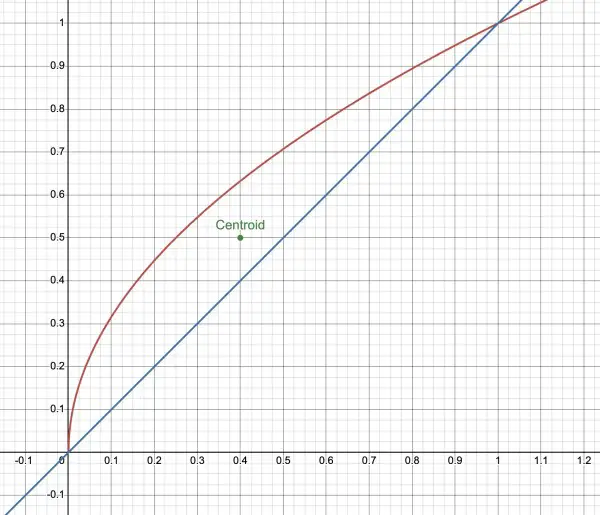
The red curve is y=√x and the blue line y=x.