Question

Find the area of the propeller-shaped region enclosed by the curves x-y^(1/3)=0 and x-y^(1/5)=0

Answer 1

The area between the red and blue lines is the area referred to in the question:

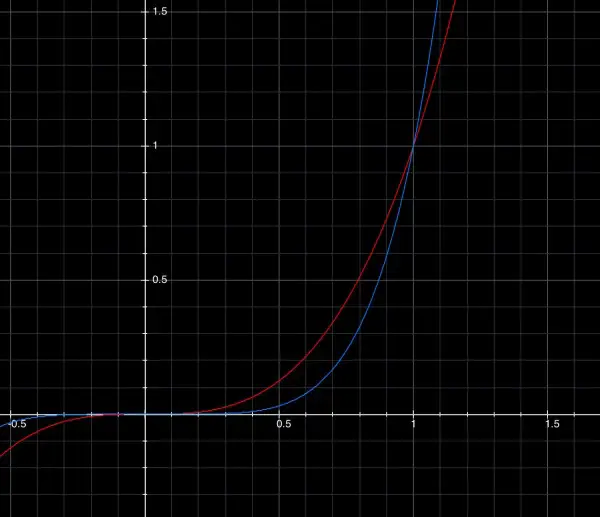
From the picture we can see the area is between x=0 and 1. So, if S[low,high](...) denotes definite integral, we have to integrate the expression x^3-x^5 between 0 and 1=S[0,1]((x^3-x^5)dx because y=x^3 (red) and y=x^5 (blue) are the given equations rewritten. We get (x^4/4-x^6/6)[0,1]=1/4-1/6=3/12-2/12=1/12.