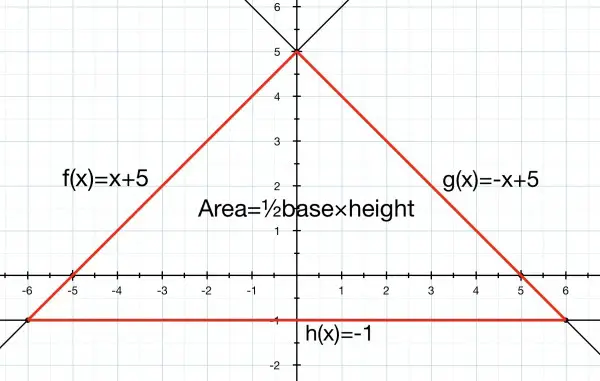
The line h(x)=-1 intersects f(x)=x+5, when -1=x+5, that is, x=-6; and intersects g(x)=-x+5, when -1=-x+5, that is, x=6. f(x)=g(x) gives the intersection of the two functions: x+5=-x+5, 2x=0, x=0. Intersection at (0,5), the common y intercept.
The beauty about this problem is that we don’t need to use integrals to find the required area since it is simply the area of the red isosceles right triangle shown above. The height is 5-(-1)=6 and the base is 6-(-6)=12. Therefore the area is ½(6×12)=36 square units.
(If you’re wondering why you can’t or don’t get the right answer using integrals it’s probably because you didn’t realise that areas below the axis are negative. You can still work it out using integrals but you need the inverse functions for f and g, that is, x in terms of y where y=f(x) or g(x), then you use ∫xdy rather than ∫ydx. If you carefully analyse the integration process for finding areas you will see why areas below the axis are negative.)