First we need to find out where the line intersects the parabola (a picture helps to visualise this problem).
x=y2+2=y+8, y2-y-6=0=(y-3)(y+2), so y=3 and -2 are the intersections. x=y+8=11, 6. The intersection points are (11,3) and (6,-2). We also need the vertex of the parabola. x=y2+2 has its vertex at (2,0) because x has its minimum value when y=0. It's also worth noting that the line intersects the x-axis (y=0) at x=8 and the y-axis at y=-8 . The picture below should help. The region enclosed by the red curve and blue line is what is to be rotated around the y-axis.
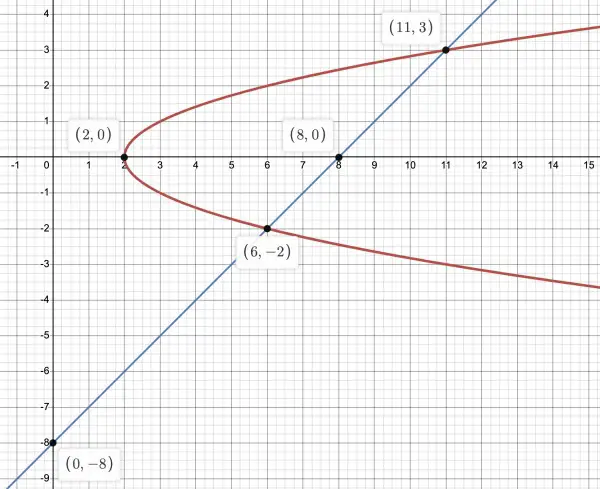
Take a thin horizontal rectangular strip between the red curve and blue line and note the endpoints: left is at (y2+2,y), right is at (y+8,y). When these points are rotated about the y-axis they create a washer (a disc with a hole in the centre), having an area=π(R2-r2) where R=y+8 and r=y2+2. If the washer has thickness dy, then its volume is π(R2-r2)dy. The sum of the volumes of many such stacked washers=
π-2∫3π(R2-r2)dy=π-2∫3π(y2+16y+64-y4-4y2-4)dy=π-2∫3π(60+16y-3y2-y4)dy=
π[60y+8y2-y3-y5/5]-23=
π[(180+72-27-243/5)-(-120+32+8+32/5)]=
π(882/5+368/5)=250π cubic units.