Find the time when the two cars are closest.

Question

Two roads OA and OB intersect an angle of 60 degrees.A car driver approaches O from A,where OA=800m, at a uniform speed of 20m/sec.
Simultaneously another car moves from O towards B at a uniform speed of 25m/sec. Find the time when the two cars are closest.

(Use differentiation)

Answer 1

After time t seconds car A (on OA) has travelled 20t metres towards O, while car B (on OB) has travelled 25t metres away from O.

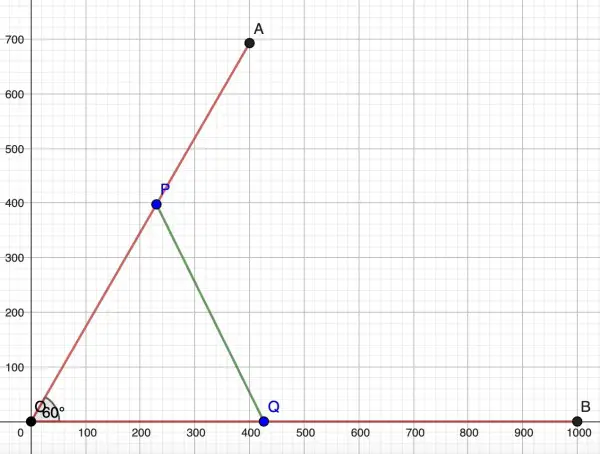
B has been arbitrarily placed on the x-axis. It's position is not relevant to the problem, except that it establshes the direction of OB. Note that triangle OPQ is not an equilateral triangle. OA=800m. PQ is the shortest distance between the cars.

NON-VECTOR METHOD

We can express the positions of A and B in the Cartesian plane x-y after time t respectively as:

P(400-10t,400√3-10t√3) and Q(25t,0).

[When t=0 car A is at point A(800cos(60),800sin(60))=A(400,400√3).

When t=0 car B is at O(0,0). At any time t, the y-coordinate remains at zero. Q stays on the x-axis.

After time t, AP=20t which reduces the y-coordinate of P by 20tsin(60)=10t√3 and the x-coordinate by 20tcos(60)=10t, hence the coordinates of P and Q above.]

The distance s between P and Q is √((400-10t-25t)²+(400√3-10t√3)²).

s=√((400-35t)²+3(400-10t)²),

s=√(160000-28000t+1225t²+480000-24000t+300t²),

s=√(640000-52000t+1525t²). This is the upper half of a hyperbola.

s²=640000-52000t+1525t², 2sds/dt=-52000+3050t.

When ds/dt=0 we have a turning point (max or min), so 3050t=52000, t=52000/3050=17.05 seconds approx. If we differentiate again we get:

2sd²s/dt²+2ds/dt=3050, but ds/dt=0 so 2sd²s/dt²=3050 and this positive value shows there to be a minimum for all t, and there is no maximum for the upper half of the hyperbola. We are only considering positive s values.

Another reason why this value of t is a minimum is that, when t=0 (starting condition) s=800m (length of OA), and when t=40 seconds (when car A reaches O) s=1000m (car B reaches point B), t=17.05 seconds is between these two time values and s=443.53m (approx), which is lower than both 800m and 1000m. This indicates that this value of t produces a minimum s.

From this value of t various other points can be calculated, for example, how far car A is from point A or O (about 341m from A, 459m from O), and how far car B is from O (about 426.2m). The graph is to scale, the numbers on the axes being metres measured north and east.