First, we need to find where the line and parabola intersect. At the intersection point the x values coincide, so:
2y2=1-y, 2y2+y-1=0=(2y-1)(y+1), so y=½ and -1 and correspondingly x=1-y=½ and 2.
The intersection points are (½,½) and (2,-1) as shown in the graph below:
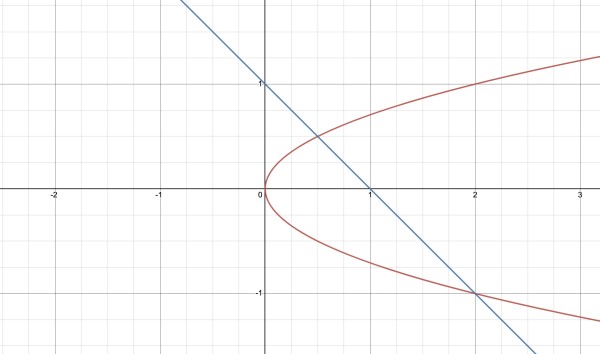
The bound region is clear to see. The principle of the exercise is to divide the area into thin rectangles. We need to find the dimensions of an arbitrary rectangle, and we can choose rectangles that are orientated horizontally or vertically. The sum of the areas of the thin rectangles is the area of the bound region; the sum of these areas is what is meant by the integral as the width of the rectangles gets so small that it's infinitesimal, and will be represented by dx or dy, depending on which way we measure length. Ideally we want the integrand to resemble f(y)dy (horizontal rectangles) because we have x in terms of y, where f(y)=x is a function of y only. The limits of the integral will be limits applied to y and determined by the intersections. So straightaway we know what the limits are: -1 to ½.
The length of a typical thin rectangle is not as easy to determine. Take a point P(x,y) on the blue line. We can write where the endpoints of the thin rectangle are. The rightmost point is on the line, so its coordinates will be (1-y,y). For example, if y=¼, x=¾. P can be expressed P(1-y,y)=(¾,¼). The leftmost point is on the parabola and has the coordinates Q(2y2,y), (⅛,¼). The length of PQ=1-y-2y2 (¾-⅛=⅝) and this is the length of the rectangle, so its area is (1-y-2y2)dy (length×width).
Let's take another example where P is below the x-axis, P(3/2,-½) is the rightmost endpoint, and Q(½,-½), making the length PQ of the rectangle 1-(-½)-2(-½)2=1+½-½=1. That's 4 squares on the graph as you can see.
So we have -1½ ∫(1-y-2y2)dy=
[y-y2/2-2y3/3]-1½=
(½-⅛-1/12)-(-1-½+⅔)=7/24-(-⅚)=7/24+⅚=27/24=9/8 square units.