y=x³-8x, y'=3x²-8.
The gradient is 3x²-8 at point x. So, at point (p,p³-8p), the equation of the tangent line is y=(3p²-8)x+a. To find a, we plug in the point: p³-8p=(3p²-8)p+a, a=p³-8p-3p³+8p, making a=-2p³, and y=(3p²-8)x-2p³. But this tangent line must also pass through the given point (1,-8), so -8=3p²-8-2p³. So 3p²-2p³=0=p²(3-2p), and p=0 or 3/2. The equations of the tangents are y=-8x (when p=0 at (0,0)) and y=(27/4-8)x-27/4=-5x/4-27/4 (when p=3/2 at (3/2,-69/8)).
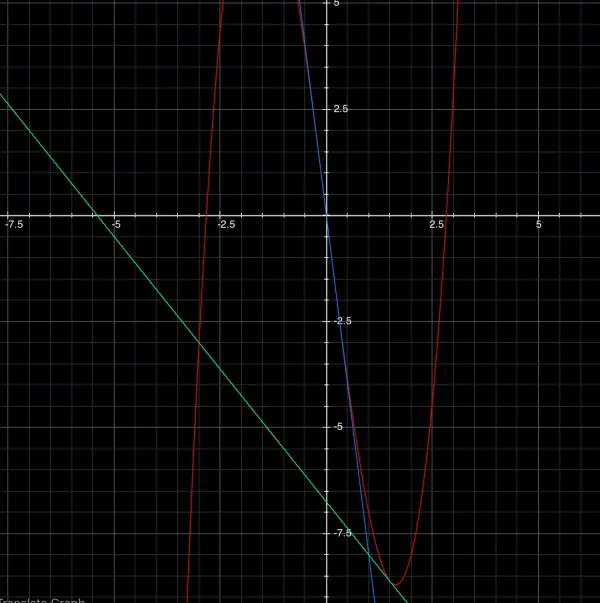
The curve is shown in red. The two tangents intersect at (1,-8) and are represented by the blue and green lines.