Find the equation of the normal plane to the curve α(t)=(e^t,cos(t),3t^2 ) at t=1.?

Question

need help on this

Answer 1

The equation of the normal plane takes the form:

a(x-x₀)+b(y-y₀)+c(z-z₀)=0 where the vector <x₀,y₀,z₀> is <e^t,cos(t),3t²> when t=1; so:

<x₀,y₀,z₀>=<e,cos(1),3>.

<a,b,c> is the normal vector of the plane, and, since the normal is perpendicular to the tangent, if we find the tangent (by differentiation of the tangent vector components), we automatically get the normal vector. (The equation of the plane is derived from the dot product of the normal n=<a,b,c> and two points with position vectors OP<x₀,y₀,z₀) and OQ<x,y,z>, PQ=OQ-OP, where O is the origin. PQ.n=0⇒a(x-x₀)+b(y-y₀)+c(z-z₀)=0.)

α(t)=<e^t,cos(t),3t²>.

The tangent vector function is α'(t)=<e^t,-sin(t),6t>. This means that the tangent in the x direction is e^t, in the y direction -sin(t), in the z direction 6t.

When t=1, we get a=e, b=-sin(1), c=6 and the equation of the normal plane is:

e(x-e)-sin(1)(y-cos(1))+6(z-3)=0. The picture below is a 3D representation of the curve with the normal plane intersecting it. Point P is the given point (t=1). You can see that P lies on the plane and the curve. The picture can be viewed using 3D glasses (green or blue filter for right eye and red for the left eye). Note how the plane intersects the curve.

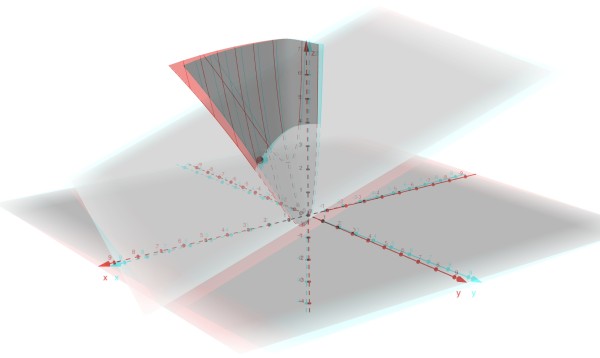
Picture by courtesy of GeoGebra Calculator Suite.