How can I show (x-10) (X+30) geometrically?

Question

How can I draw it?

Answer 1

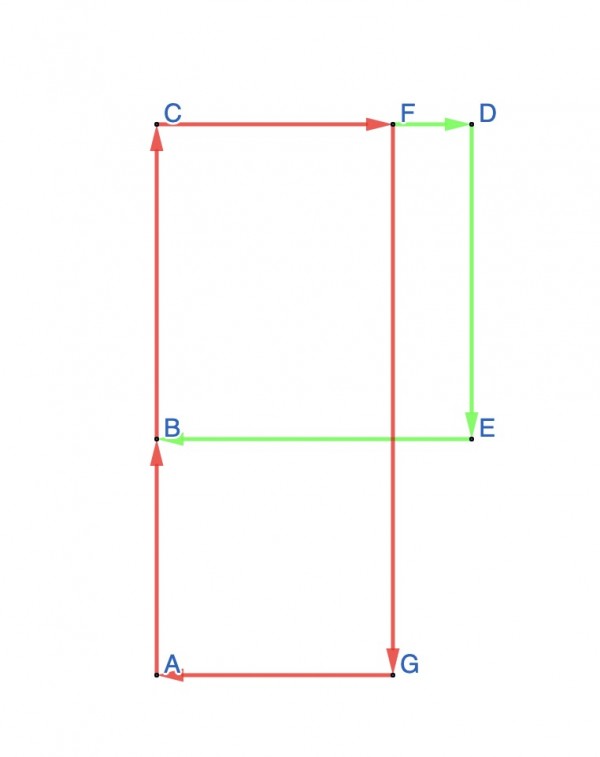
In the picture, BCDE represents a square with side length x. FD has length 10 and AB has length 30.

Therefore CF=x-10 and AC=x+30. The red rectangle ACFG has area (x-10)(x+30). This is one way to represent this algebraic product geometrically.

If we expand the expression we get x²+20x-300. x² is the area of BCDE. The area of the top part of ACFG=x²-10x (the area of square BCDE less the area of the thin green strip, DE=x, FD=10, area=10x). The area of the lower part of ACFG=30(x-10)=30x-300 (AB=30, AG=x-10). Therefore the area of ACFG=x²-10x + 30x-300=x²+20x-300. So the geometry confirms the algebraic product.