To prove/disprove graphically:
- Label quadrilateral ABCD, A(0,0), B(b1,b2), C(c1,0), D(d1,d2) (diagonal AC lies arbitrarily on x-axis to simplify calculations)
- Coords of mid-points are average of coords of vertices, e.g., N((b1+c1)/2,b2/2) is the mid-point of BC, etc. Calculate coords of the 4 mid-points
- Use these to calculate the slopes of the mid-segments (diff of y coord/diff of x coord). Observe that opposite mid-segments have same slope, so we have a parallelogram at least
- Calculate lengths of mid-segments using Pythagoras and the differences between the mid-point coords
You have all that’s needed to prove whether or not the parallelogram is a rhombus (mid-segment lengths of at least two adjacent sides are equal).
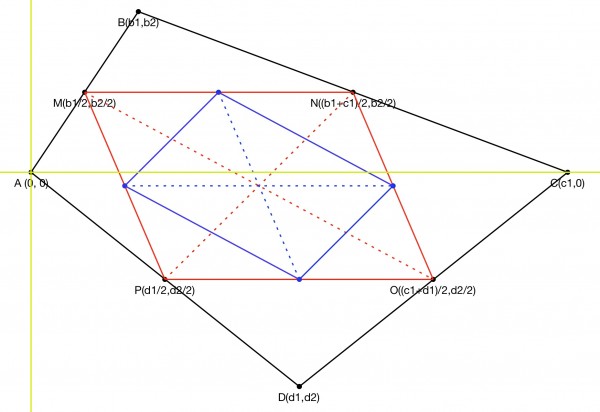
This picture shows that for a general quadrilateral ABCD, the mid-segments form a parallelogram MNOP (red) but not a rhombus (the diagonals, shown as dotted red lines do not intersect at 90°). Even the parallelogram (blue) formed by the mid-segments of the parallelogram do not form a rhombus. The Cartesian axes are shown in lime green.
(Geometrically, if the quadrilateral’s diagonals are used to split it into two pairs of triangles, the midsegment theorem shows that, only if the diagonals have the same length, can the figure be a rhombus.)