show that the points a (3,4) b(3,1) and c (8,4) are vertices of a right angle triangle. Find the length of the perpendicular from A to BC

Question

this is a question from coordinate geometry related to length of line segment

Answer 1

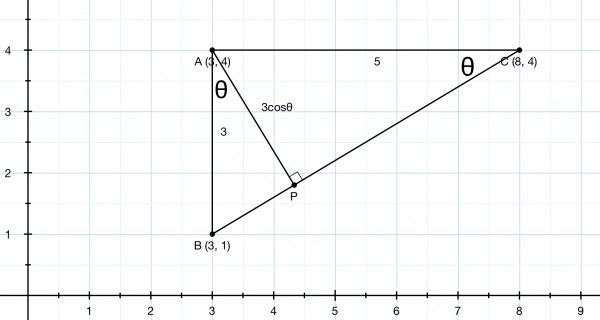
A and B have the same x coord, so AB is vertical. AB has length 4-1=3.

A and C have the same y coord, so AC is horizontal. AC has length 8-3=5 and A is the right angle. ABC is a right triangle.

Let the perpendicular be AP where P is on BC.

We have 3 similar triangles: ABC, PBA, and PAC, because A and P are right angles, ∠ABP=∠BCA, ∠ABP=∠PAC.

Let θ=∠C then tanθ=AB/AC=3/5. From Pythagoras’ Theorem, BC=√(AB²+AC²)=√(3²+5²)=√34 and cosθ=AC/BC=5/√34.

AP=ABcosθ=ACsinθ=15/√34=2.5725 approx.

You don’t need to use trigonometry to solve this, you can just use the side ratios: 3/5 in place of tanθ, 3/√34 in place of sinθ, and 5√34 in place of cosθ, and apply the rules for similar triangles.