Question

shortest distance between line y-x=1 and curve x=y square

Answer 1

The slope of the line y-x=1 or y=1+x is 1 (angle of 45°).

When the tangent of the parabola is parallel to the line the perpendicular between the line and the tangent to the curve is the shortest distance.

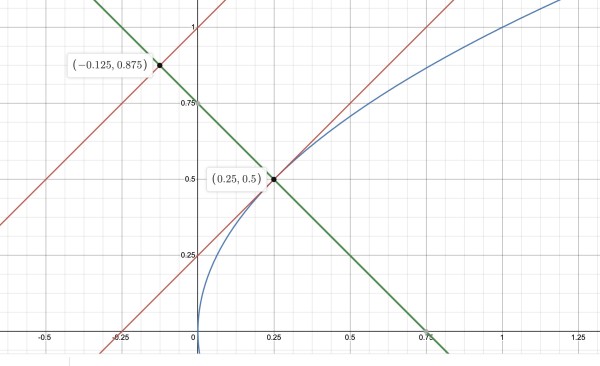
If we differentiate x=y² wrt x we get 1=2ydy/dx. dy/dx=1 means the tangent is 1 when 2y=1, y=½.

x=y²=¼. So the normal at (¼,½) has a slope of -1 and the equation of the normal is:

y-½=-(x-¼) which can be written 4y-2=-4x+1, 4x+4y=3.

This normal intersects the line y=1+x when:

4x+4(1+x)=3, 4x+4+4x=3, 8x=-1, x=-⅛, so y=⅞. The intersection point is (-⅛,⅞).

The shortest distance is found using Pythagoras' Theorem:

√((¼-(-⅛))²+(½-⅞)²)=√(⅜²+⅜²)=√(9/32)=√(½×9/16)=¾/√2=⅜√2=0.5303 approx.