equation of the line that is an equal distance between points (3,10) and (13,4)

Question

a committeeis choosing a site for a county fair, The site needs to be located the same distance from the two main towns in the county. on a map these towns have coordinates (3,10)  and (13, 4) . Determine an equation for the line that shows all possible sites for the fair 

Answer 1

First locate the midpoint which is the average of the coords: ((13+3)/2,(4+10)/2)=(8,7).

Now we need the equation of the perpendicular. Slope of line joining the points=(4-10)/(13-3)=-6/10=-0.6.

Slope of perpendicular=-(-1/0.6)=5/3. Equation of perpendicular: y-7=5(x-8)/3, y=5x/3-40/3+7, y=5x/3-19/3, or 3y=5x-19. For example, (5,2) lies on this line and is equidistant from the two given points because we have an isosceles triangle and we just drew the perpendicular bisector of the base to a vertex. Because the sides of an isosceles triangle are of equal length, the distance from each of the two given points will be the same for all points on the line 3y=5x-19.

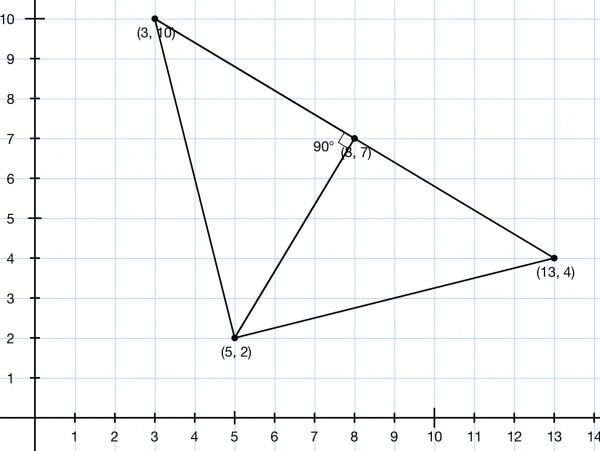
Note that the line is a continuation of the perpendicular bisector. The picture just shows the formation of one particular isosceles triangle where (8,7) and (5,2) are only examples of points equidistant from the two given points (towns).