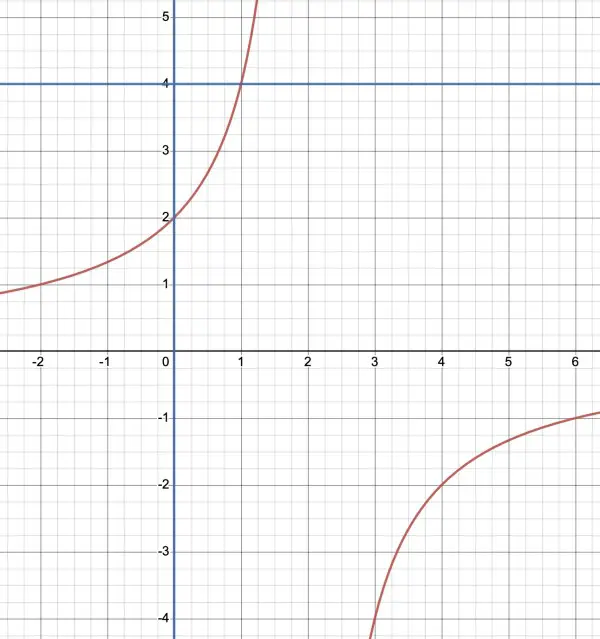
The required area is bounded by the red curve (g(x)) and the two lines in blue (x=0 is the y-axis, y=4 is the horizontal line).
The area is found by an integral. The curve intersects the y-axis when y=g(0)=4/2=2, the y-intercept or point (0,2). It intersects the curve when g(x)=4, that is, 4/(2-x)=4, 2-x=1, x=1, that is, the point (1,4).
Imagine the area to be divided into narrow vertical rectangular strips. The leftmost strip has a length of 4-2=2. For any x between 0 and 1 the length of the strip will be 4-g(x)=4-4/(2-x). If the width of the strip is dx, then the area of the strip is [(4-4/(2-x)]dx which is the integrand. Integrating, we get: 4x+4ln(2-x) for 0≤x≤1=(4+4ln(1))-(0+4ln(2))=4-4ln(2)=1.2274 square units approx.