y=x^2-1, y=-x+2, x=0, x=1

Question

sketch the region bounded by the graphs of the algebraic functions and find the area of the region

Answer 1

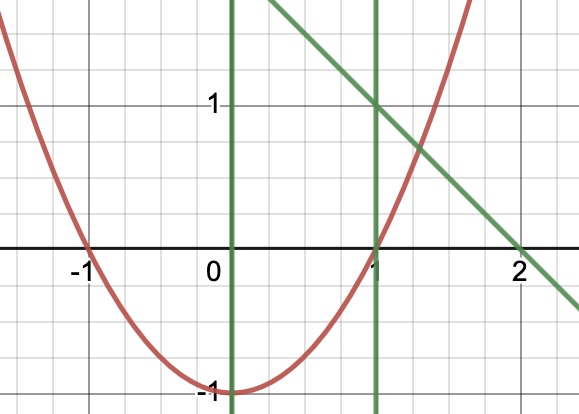
The required region is bounded by 2 green lines (x=1 and y=-x+2) and a red curve, y=x²-1.

The picture shows that the curve and the lines intersect, the vertical x=1 when y=x²-1=1-1=0, the point (1,0).

The other intersection point is when -x+2=x²-1, x²+x-3=0, x=(-1+√13)/2 (the negative solution of this quadratic is ignored because it's outside the region).

So the area extends from x=1 to x=(-1+√13)/2. Imagine thin rectangular strips constituting the region so that the sum of the areas of the strips is the area of the region.

The leftmost strip has a length of 1. If we take some arbitrary value of x between 1 and (-1+√13)/2, the length of the strip will be 2-x-(x²-1)=3-x-x². The width of the strip is dx for each strip.

The area of the strip is (3-x-x²)dx which is the integrand for a summation of infinitesimally thin strips. Integrating: 3x-½x²-⅓x³ for 1≤x≤(-1+√13)/2.

The upper value of this expression is 2.32268 approx. For the lower value it's 13/6=2.16667. The difference is the area of the region: 0.156 square units approx.