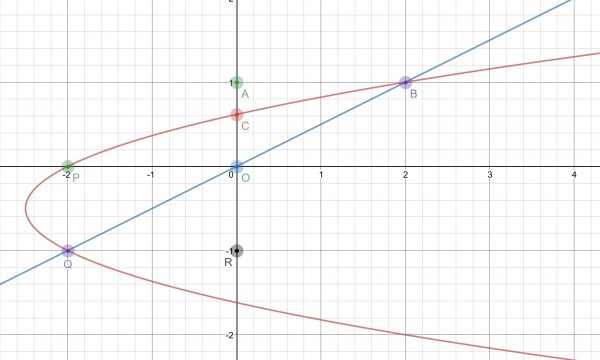
The first task is to find out where the curve and straight line intersect.
We find this by putting x=2y into the quadratic and solving for y:
2y²+2y-2y-2=0, 2y²=2, y²=1, so y=±1. Knowing y we can find corresponding x values and arrive at the intersection coordinates: (2,1) and (-2,-1).
We also need to find out the y intercepts by putting x=0 and solving for y:
2y²+2y-2=0, y²+y-1=0, y=½(√5-1), -½(√5+1).
The picture shows the area between the line and curve we have to find. Some important coordinates have been labelled.
Part of the area we need to calculate is to the left of the y axis, and that area will be calculated as negative. So we need to calculate the area to the right of the y axis and the area to the left separately, otherwise we’ll end up by subtracting areas we need to add. We’ll need to perform two separate integrations. We use ∫xdy with appropriate limits, because we can easily express x in terms of y, but y in terms of x would involve square roots, and that would not be so easy. So x=2y²+2y-2. On integrating this with respect to y we get:
2y³/3+y²-2y. Now we need the limits for various areas. The areas will be in relation to the y axis, not the x axis. Parts of the areas are areas of simple geometric figures for which no integration is needed.
I hope to make it absolutely clear how the areas can be calculated. We’ll be using the areas of right triangles AOB and ROQ, both with area 1 square unit.
(1) Area COB=area AOB-area ACB, where area ACB=∫xdy for the interval [½(√5-1),1].
(2) Area COP=∫xdy for the interval [0,½(√5-1)], which will be negative because it lies to the left of the y axis, so we reverse the interval: [½(√5-1),0] to get a positive area.
(3) Area OPQ=∫xdy[-1,0]-area ROQ.
The sum of areas (1), (2) and (3) is the total area between the curve and straight line. Areas to 4 decimal places ([low,high] denotes interval):
(1) Area COB=1-(2y³/3+y²-2y)[½(√5-1),1]=
1-[(-⅓)-(7-5√5)/6]=(15-5√5)/6=0.6366.
(2) Area COP=(2y³/3+y²-2y)[½(√5-1),0]=(5√5-7)/6=0.6967.
(3) Area OPQ=(2y³/3+y²-2y)[-1,0]-1=(-⅔+1+2)-1=4/3=1.3333.
Sum of these areas=(15-5√5)/6+(5√5-7)/6+4/3=4/3+4/3=8/3.