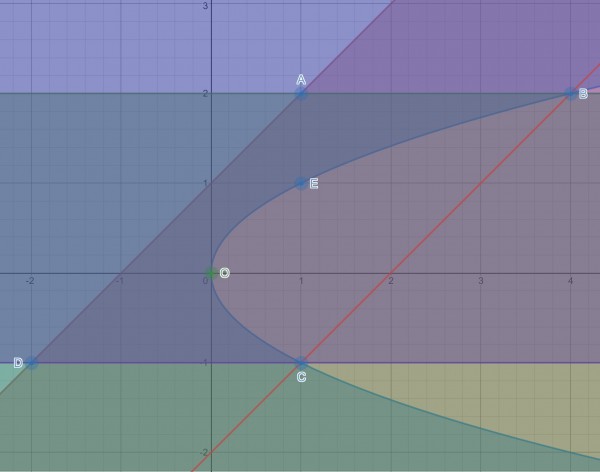
y=x+1 intersects horizontal y=2 at A(1,2).
y²=x intersects y=2 at B(4,2).
y=x+1 intersects y=-1 at D(-2,-1).
y²=x intersects y=-1 at C(1,-1)
ABCD is a parallelogram with base DC=AB=1-(-2)=3 and height 2-(-1)=3. The equation of BC, parallel to AD, is y+1=x-1, (passing through (1,-1)), that is, y=x-2.
E(1,1) and O(0,0) complete the geometry for this problem.
Right triangle ACD has area=½AC.DC=½(3)(3)=9/2 square units.
The arc COE of the parabola cuts into ∆ACD. The area enclosed by the parabola and the line EC can be calculated as 2∫ydx in the interval [0,1] because of symmetry and substituting y=√x. So 2∫√xdx=2(⅔)[x^(3/2)]¹₀=4/3 square units. Therefore, 9/2-4/3=19/3 square units is the contributory area to the left of x=1.
The remaining area is bounded by the curve arc EB, the lines x=1 and y=2 in the x interval [1,4].
The integral is ∫(2-√x)dx=[2x-⅔x^(3/2)]⁴₁=(8-16/3)-(2-⅔)=8/3-4/3=4/3.
The total area is 19/3+4/3=23/3 square units.