Let the tree's height be represented by the line GT where G is the ground base and T the top of the tree.
TÂG=TÂB=40°, TB̂G=58°, therefore since TB̂G=TÂB+BT̂A as the exterior angle of triangle TAB, BT̂A=58-40=18°. Because GT is vertical, TĜB=90-18=72° and GT̂B=180-(TĜB+TB̂G)=180-(72+58)=50°. AB=60ft.
Sine Rule:
AB/sinBT̂A=TB/sinTÂB, TB=ABsinTÂB/sinBT̂A=60sin40°/sin18°;
GT/sinTB̂G=TB/sinTĜB, GT=TBsinTB̂G/sinTĜB=TBsin58°/sin72°,
GT=(60sin40°/sin18°)(sin58°/sin72°)=60sin40°sin58°/(sin18°sin72°)=111.29ft approximately.
(Since sin72°=cos18°, sin18°sin72°=sin18°cos18°=½sin36°, so we could have used GT=120sin40°sin58°/sin36°.)
So the height of the tree (GT)=111.29ft.
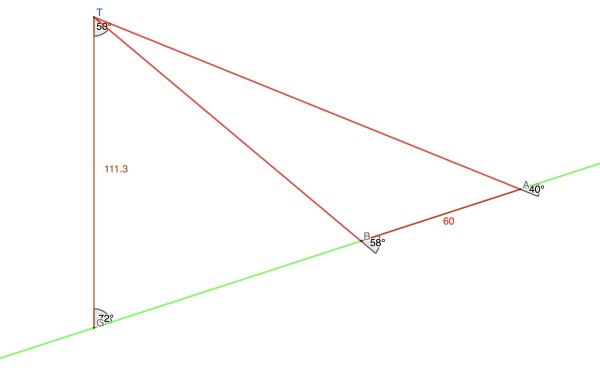
The green line represents the hill inclined at 18° to the horizontal.