Calculus Two

Question

 

A bug

crawls on

the plane

푧푧

=

2

푥푥

+

푦푦

, from

the

point (

–2, 4, 0

) to the point (2, 4, 8)

along a path

whose

projection down on the

x

-y

plane is the parabola

푦푦

=

푥푥

2

(

−

2

≤푥푥 ≤

2

)

.

You

r job is to find

the points at which its path is

most steep or least steep, where steepness is

measured as the absolute value of the slope (as usual

z

is the vertical axis).

(a) Provide a technic

al analysis, finding the

maxim

um and a minimum of

|

m

| where

m

is

the slope of

its path.

(b)

Explain how your solution could be obtained from a careful examination of the interaction

between the bug’s path and the contour lines of the plane. You must include

a diagram with your

explanation.

A bug

crawls on

the plane

푧푧

=

2

푥푥

+

푦푦

, from

the

point (

–2, 4, 0

) to the point (2, 4, 8)

along a path

whose

projection down on the

x

-y

plane is the parabola

푦푦

=

푥푥

2

(

−

2

≤푥푥 ≤

2

)

.

You

r job is to find

the points at which its path is

most steep or least steep, where steepness is

measured as the absolute value of the slope (as usual

z

is the vertical axis).

(a) Provide a technic

al analysis, finding the

maxim

um and minimum of

|

m

| where

m

is

the slope of

its path.

(b)

Explain how your solution could be obtained from a careful examination of the interaction

between the bug’s path and the contour lines of the plane. You must include

a diagram with your

explanation.

Answer 1

 

 

z=2x+y and y=x²⇒z=x²+2x.

dz/dx=2x+2=0 at an extremum, so solving for x, x=-1. m=dz/dx increases as x increases from -1. (When x<-1, m<0. At (-2,4,0), m=-2, |m|=2. At (2,4,8), |m|=m=6.)

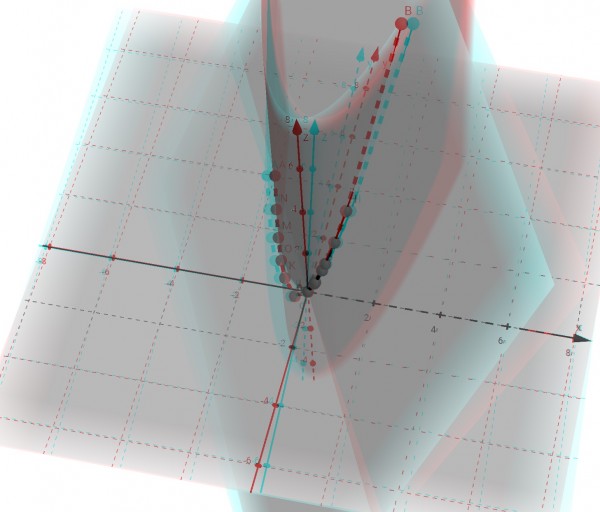
Therefore the point (-1,1,-1) is an extremum. This is a minimum because the starting point (-2,4,0) is in the x-y plane and (-1,1,-1) is below this plane. Also, the crawl path passes through the origin (0,0,0). The bug’s path from (-2,4,0) to (2,4,8) dips below the x-y plane to the minimum point (-1,1,-1), rises through the origin, and proceeds along the curve z=x²+2x. In the 3D picture (best viewed using 3D glasses, right eye green or blue, left eye red), points on the parabola z=x²+2x are emphasised by the labelled “beads” strung along the crawl path, where A is the start and B the finish. Bead K is the minimum. The projection of the parabola z=x²+2x on to the x-y plane is y=x², and is shown as an upright extrusion of the parabola y=x². Effectively, the plane z=2x+y slices through the extruded parabola to produce the beaded path.

|m|=0 is minimum and |m|=6 is maximum.