trace the curve y^2 (x^2-9)=....... (Calculus)

Question

Trace the curve.... y^2(x^2-9)=x^4.... by stating all the properties used in tracing.....

Answer 1

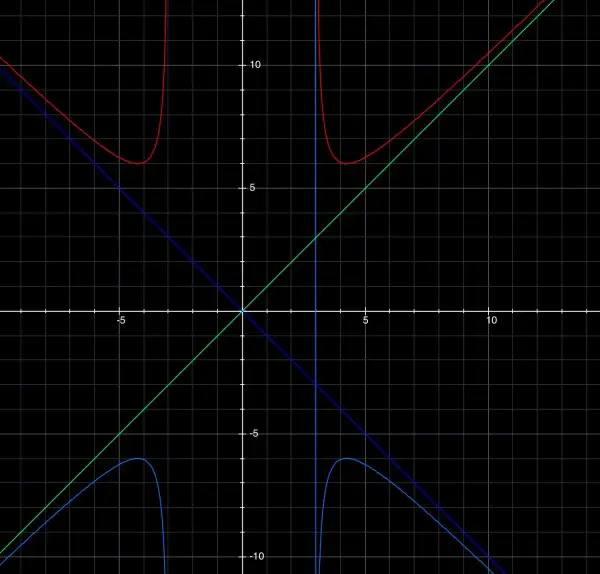
The curve does not exist for -3<x<3 because there can be no solutions for y when x^2<9.

Because of the presence of x^2 and y^2 the curve is essentially reflected in all quadrants. If we examine QI only we have the same patterns reflected in the other quadrants. x=-3 and x=3 are asymptotes.

As x gets larger, the constant 9 becomes more insignificant and y^2 becomes x^2, in other words, the curve in QI has an asymptote y=x, which is reflected in all the other quadrants. So we know the curve is trapped between the vertical asymptote and the line y=x.

(2ydy/dx)(x^2-9)+2y^2x=4x^3 is the derivative. When dy/dx=0, there is a turning point. y^2=2x^2. That is, x^4/(x^2-9)=2x^2. x^4=2x^4-18x^2; x^2=2x^2-18; x^2=18, x=3sqrt(2) and y^2=36, so y=6. In QI then, there is a turning point at (3sqrt(2),6). This is reflected in each quadrant. This is a minimum (in QI) because the curve is trapped between the above asymptotes. There is enough information now to trace the curve(s). The asymptotes resemble a cross intersected by vertical lines. The asymptote in QI and QIV has been drawn in to illustrate how close the curve comes to it.

 

Comments

What are the properties of tracing?? (just for my knowledge)

---

The properties are the properties of the function given:

• Where is the function defined (domain and range)? These give a clue to the shape.
• Are there any extrema? Maximum and minimum points are useful in tracing.
• Are there any asymptotes? These help to define the constraints for the curve. They can also be drawn on to the graph to show where the curve approaches them.
• Is the curve constinuou? Are there any holes or discontinuities?
• What is the behaviour for large values of the variables? (This can help to define asymptotes.)
• Is the curve reflected (usually even exponents give rise to the same quantities for positive and negative values)?

All these properties define the behaviour of a curve and help to trace (sketch) it.