13. Area=25±0.06 sq in. Minimum value is 24.94 and maximum value is 25.06.
√24.94=4.994 and √25.06=5.006 in. So the side length is 5±0.006 in, which is within 0.006 in of 5 in.
This is an arithmetic approach. Now we’ll look at an algebraic approach.
Let side length be x, and h=difference in x corresponding to a difference k in the area:
(x+h)²=25±k, x²+2hx+h²=25±k. When x=5, 10h+h²=±k, but when h is small we can ignore h², so h=±k/10=±0.06/10=±0.006 in when k=±0.06 sq in. This means that each piece of wire must be within 0.006in of 5 inches.
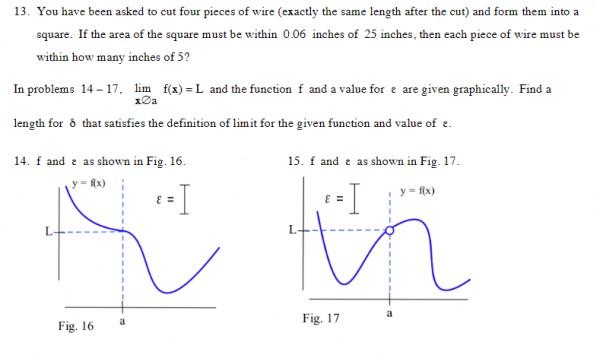
14. Variation in L is given by L±ɛ and variation in x by x±∂. f(x±∂)=L±ɛ and x➝a so f(a±∂)=L±ɛ. [This means that f(a-∂)=L-ɛ and f(a+∂)=L+ɛ.] Also, f(a)=L and ɛ=f(a+∂)-f(a) and ɛ=f(a)-f(a-∂).
When f is differentiable at x=a, f'(x)=df/dx≈ɛ/∂ at x=a. Therefore ∂≈ɛ/f'(a).
Lim as ɛ➝0 (f(a+∂)-L)/ɛ=1. Since x➝a then x-a➝0⇒∂➝0 because x=a+∂.
Lim ∂➝0 f(a+∂)=L=f(a) or Lim ∂➝0 f(a+∂)-L=0.
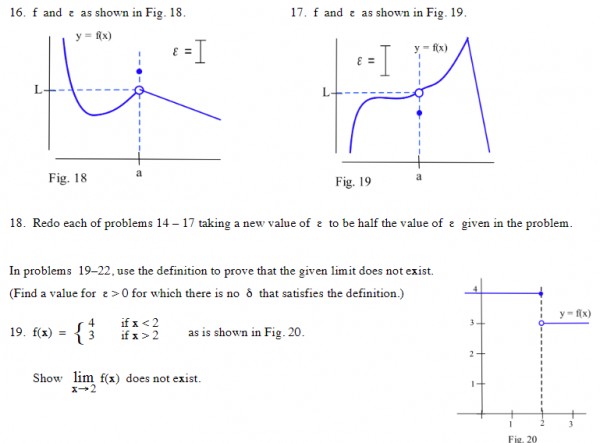
In 15, 16 and 17 the limit still applies because the left and right limits for x➝a are equal despite the fact that f(a) itself is specifically defined. We are only interested in x➝a, not x=a.
18. If ɛ is halved ∂ is also halved because the value of f'(a) is constant.
19. The left limit is 4 and the right limit is 3. Since these are different there is no limit for x➝2, that is, it cannot be defined or does not exist. Even if there were a value for x=2 (as indicated on the graph), the limit remains undefined.