Rewrite the DE:
u''(x)-u(x)=-910x.
The characteristic equation is found by solving r²-1=0. (r represents u'').
So r=±1, giving us u₁=Ae⁻ˣ+Beˣ, where A and B will be found later from the initial conditions.
The particular equation we can guess has the form u₂=ax+b, where we can work out constants a and b:
u₂'=a and u₂''=0, so the DE becomes:
0-ax-b=-910x, from which b=0 and a=910, making u₂=910x.
The complete solution is u₁+u₂=u=Ae⁻ˣ+Beˣ+910x.
But u(0)=0=A+B, so B=-A.
u(1)=A/e-Ae+910=0, A-Ae²+910e=0.
From this A=910e/(e²-1)=387.1677 approx.
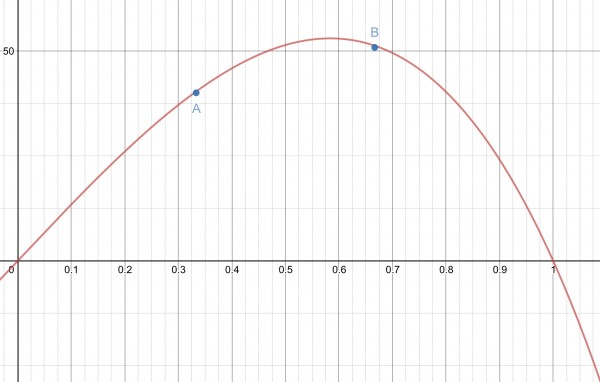
Therefore u=387.1677e⁻ˣ-387.1677eˣ+910x. In the graph below you only need the “hump” between x=0 and x=1. This will be the region divided into segments of equal length.
Another way if writing this is:
u(x)=910x-(910e/(e²-1))sinh(x).
[sinh(x)=½(eˣ-e⁻ˣ)]
Now, using the finite element method, we get:
d²u/dx²-u=-910x.
Divide (0,1) into n equal segments, so each segment has length=1/n. Call this length ∆x. The division gives rise to nodes numbered 1 to n+1.
If n=3, so ∆x=⅓ and 1≤i≤4, where i is the node number. The value of x at each node is xᵢ₋₁ and the corresponding u value is uᵢ₋₁. This means that the first node is at x=0 and the sixth node is at x=1.
x₀=0, x₁=⅓, x₂=⅔, x₃=1.
Now consider the series:
(x₀,u₀), (x₁,u₁), (x₂,u₂), (x₃,u₃).
Since xᵢ₊₁-xᵢ=∆x, the first differences (differential or derivative) are:
(u₁-u₀)/∆x, (u₂-u₁)/∆x, (u₃-u₂)/∆x.
The second differences are:
(u₂-u₁-u₁+u₀)/(∆x)²=(u₂-2u₁+u₀)/(∆x)²,
(u₃-2u₂+u₁)/(∆x)².
From which we can make the approximation:
d²u/dx²≈(uᵢ₊₁-2uᵢ+uᵢ₋₁)/(∆x)².
The boundary conditions are u₀=0 and u₅=0 (because u(0)=u(1)=0).
The DE can now be written:
(uᵢ₊₁-2uᵢ+uᵢ₋₁)/(∆x)²-uᵢ=-910xᵢ, or 9uᵢ₊₁-19uᵢ+9uᵢ₋₁=-910xᵢ, since (∆x)²=1/9.
Therefore, we arrive at a system of 2 equations:
9u₂-19u₁=-910/3, so u₂=(19u₁-910/3)/9;
-19u₂+9u₁=-1820/3, so -19(19u₁-910/3)/9+9u₁=-1820/3,
-361u₁/9+17290/27+9u₁=-1820/3.
Multiplying through by 27:
-1083u₁+17290+243u₁=-16380,
-840u₁+33670=0, u₁=33670/840=481/12=40.083.
u₂=611/12=50.917.
So the points to plot are A(⅓,481/12) and B(⅔,611/12).
These compare with u(⅓)=40.415 and u(⅔)=51.345.