Plug in the given values:
14=3[9cos⁻¹((3-h)/3)-(3-h)√(6h-h²)].
Let f(h)=3[9cos⁻¹((3-h)/3)-(3-h)√(6h-h²)]-14.
We need to identify two values, a and b, of h such that f(a)<0 and f(b)>0.
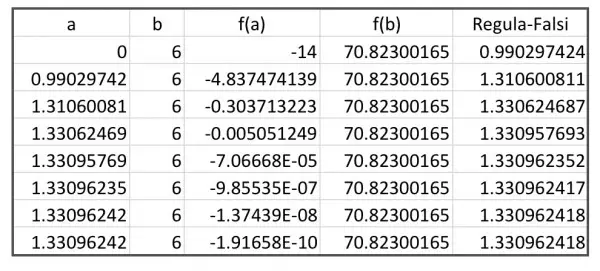
We can limit a and b by noting that 6h-h²≥0, that is, h(6-h)≥0, because the square root only applies to positive quantities. Therefore 0≤h≤6. The inverse cosine function also has a restricted argument which gives us the same range for h. Let a=0, b=6 and f(0)=-14 and f(6)=70.823 approx.
Applying the Regula-Falsi formula for the root:
h=af(b)-bf(a))/(f(b)-f(a))=-6f(0)/(f(6)-f(0))=84/(70.823+14)=0.9903 approx.
f(0.9903)<0, so we know that the root lies between 0.9903 and 6. Readjust a to 0.9903 and leave b=6.
Next estimate for h:
h=(0.9903f(6)-6f(0.9903))/(f(6)-f(0.9903))=
(0.9903×70.823-6×(-4.8375))/(70.823+4.8375)=1.3106.
f(1.3106)<0, so the root now lies between 1.3106 and 6. Readjust a to 1.3106 and leave b=6.
We continue this procedure until we reach a value of h which is stable to a sufficient number of decimal places and we end up with h=1.33096242.
Rounded to 4 decimal places this is h=1.3310.