NEWTON’S INTERPOLATING POLYNOMIAL
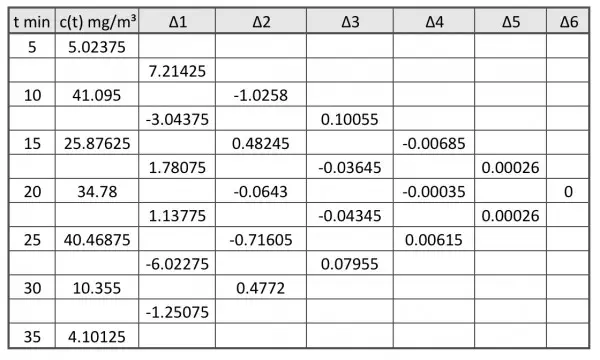
c(t)=5.02375
+7.21425(x-5)
-1.0258(x-5)(x-10)
+0.10055(x-5)(x-10)(x-15)
-0.00685(x-5)(x-10)(x-15)(x-20)
+0.00026(x-5)(x-10)(x-15)(x-20)(x-25).
Calculation of deltas (examples):
∆1=∆c/∆t=(41.095-5.02375)/(10-5)=7.21425.
∆2=(-3.04375-7.21425)/(15-5)=-1.0258.
...
∆5=(-0.00035-(-0.00685))/(30-5)=0.00026.
To get the denominators for the deltas, move along the diagonal downwards to get the t value alongside the corresponding c value and subtract the t value found by moving along the diagonal upwards alongside the corresponding c value. The downward diagonal for ∆5 (row 6), for instance, takes you to c=10.355, corresponding to t=30; the upward diagonal takes you to c=5.02375, corresponding to t=5; so the divisor (denominator) is 30-5=25.
When t=32.5, c(t) from the polynomial=-5.7528125mg/m³. Because this is negative it is not meaningful. It seems to indicate that Newton’s polynomial is not helpful in this case.
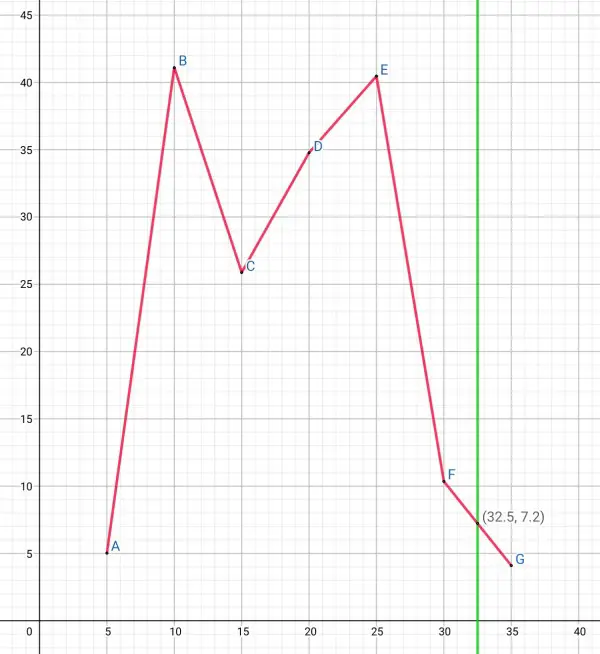
The above graph shows a probably more realistic value of 7.2mg/m³ at t=32.5min by simple interpolation.