dy/dx=4y-1; separate the variables: dy/(4y-1)=dx, integrating: (1/4)ln(4y-1)=x. ln(4y-1)=4x. The general solution is 4y-1=Ae^4x, y=(Ae^4x + 1)/4 [CHECK: y'=Ae^4x=4y-1.] Initial condition, y(0)=1: 1=(A+1)/4, A+1=4, A=3 and y=(3e^4x + 1)/4. y(0.5)=(3e^2+1)/4=5.79. This is the value we hope to approximate using Euler's method of iterative increments.
USING EULER'S METHOD
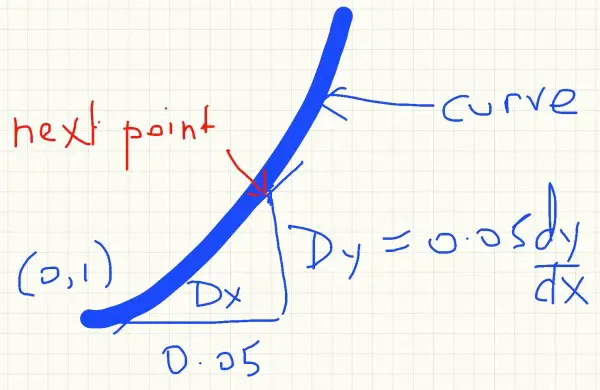
This method uses the approximation that Dy/Dx = dy/dx where D is a small increment, Dx=h=0.05. Initially y=0 and x=1. This is our starting point
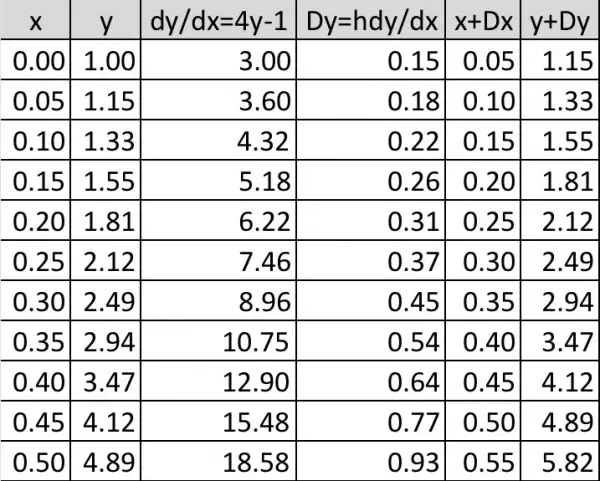
The table shows the iterative procedure. By Euler's method y(0.50)=4.89, compared with the actual value of about 5.79. The value 5.82 is in fact closer and this is the value we should use for the following reason.
The starting point is (0,1). The next x-value is the first increment giving us the horizontal base of a triangle. The end points in this base are (0,1) and (0.05,1). So the vertical height of the triangle is found by multiplying the gradient dy/dx by the increment to give us the y increment. The table then has to be interpreted by adding the increment 0.05 to the the limiting value of x, which is 0.5, making it 0.55 and reading off the corresponding y value, 5.82 (columns 4 and 5). This is the solution, y(0.5)=5.82 using Euler's method. If the increment is made smaller y(0.5) gets closer to the actual value. The picture below shows the idea. Joining the hypotenuses of these little triangles gives us an approximation to the shape of the curve.