Volume of cone=⅓πr²h=10/3 cubic units, so r²=10/(πh), where r=radius and h the height. This equation will be used later for substituting for r².
Consider a circle radius L from which a sector has been cut, with sector angle θ. This represents the mantle of a cone with slant length L. The arc of the sector has length Lθ. The radius of the base of the cone r is given by:
2πr+Lθ=2πL, that is, the circumference of the base plus the length of the sector arc makes up the circumference of the circle from which the mantle was made. From this, θ=2π(L-r)/L.
The area A of the sector is given by A/(πL²)=θ/2π, that is, the ratio of the sector angle to 2π (full revolution) is also the ratio of the area of the sector to the area of the circle from which the mantle has been made. So A=L²θ/2=πL(L-r) and the area of the mantle=πL²-πL(L-r)=πLr.
Looking at the assembled cone, from Pythagoras’ Theorem it can be seen that h²+r²=L², because the cross-section of a right circular cone is a right triangle, with legs r and h and hypotenuse L. The area of the mantle can be written:
πr√(r²+h²)=√(π²r⁴+π²r²h²)=√(100/h²+10πh) by substituting for r². The cost of the mantle at $1 a square unit is numerically the same as this expression. The cost of the base is $πmr²=$(10m/h).
The total cost C of the cone=10m/h+√(100/h²+10πh).
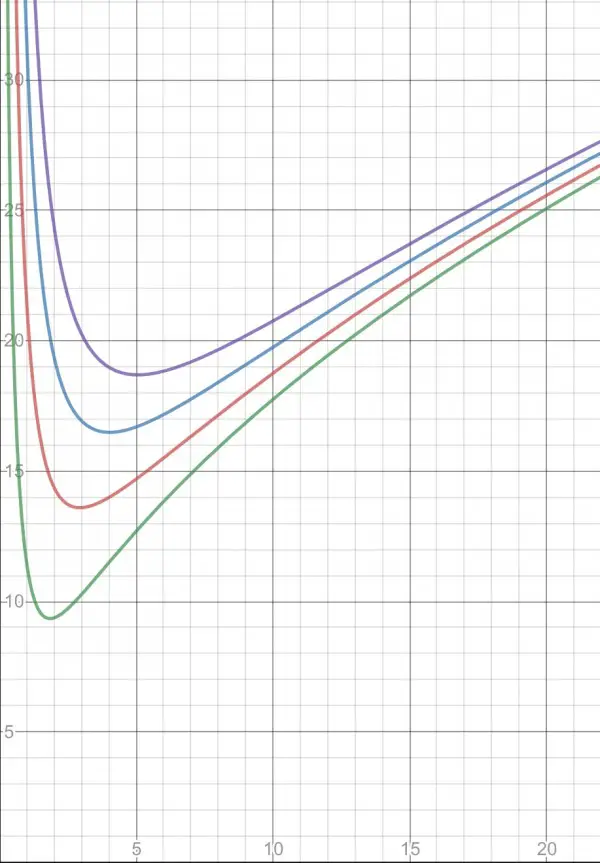
The colour-coded curves represent different values of m: 0=green, 1=red, 2=blue, 3=purple.
This can be differentiated:
dC/dh=-10m/h²+(-100/h³+5π)/√(100/h²+10πh).
At the minima shown graphically, dC/dh=0:
-2m√(100/h²+10πh)/h²=20/h³-π,
-2m√(100+10πh³)=20-πh³,
4m²(100+10πh³)=400-40πh³+π²h⁶.
When m=0, h=∛(20/π)=1.8534, r=1.3105 approx (C=9.3455).
When m=1, 400+40πh³=400-40πh³+π²h⁶, 80=πh³, h=∛(80/π)=2.942, r=1.04 (C=13.596).
The above addresses parts (a) and (b) with two values of m from the set.
(c) The graphs (blue and purple) show that the minimal cost rises as m increases.
(d) Rewrite C=(10/h)[-|m|+√(1+πh³/10)] for m<0.
If C<0, -|m|+√(1+πh³/10)<0, |m|>√(1+πh³/10), so m²>1+πh³/10. Since h>0, m<-1.