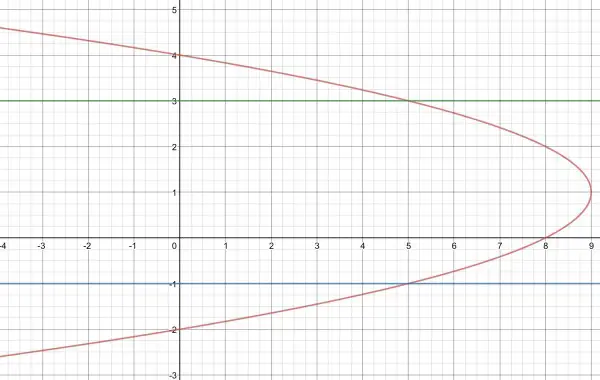
This is the graph (red) with the enclosing horizontal lines in blue and green. Important intersection points are (0,4), (0,-2), (5,3), (5,-1), (8,0), (9,1).
The question doesn’t state what all the limits are, so I assume it’s the area between the curve, the horizontal lines and the y-axis. However, x=5 could be the left hand limit. Therefore, I’ll calculate two areas: the rectangular area between the y-axis and x=5: 20 square units. The other area is from x=5 to x=9.
Given that areas below the x axis will be calculated as negative, the area between x=5 to x=9 needs to be split into the two parts: above the axis and below the axis. However, the curve is symmetrical and the axis of symmetry is y=1, so we can find the area above y=1 and double it to get the whole area.
Area=2∫(x-5)dy=2∫(3+2y-y²)dy for y in [1,3]. We need to subtract 5 from x because we are summing the area from x=5.
Area=2[3y+y²-⅓y³] for y in [1,3].
Area=2[(9+9-9)-(3+1-⅓)=2(9-11/3)=32/3.
We may need to add in the rectangular area: 32/3+20=92/3.