what is the area of 50' x 149.24' x 177.56' x 125.54 x 163.54

Question

I am trying to figure out the square footage and acreage of our lot.

Comments

We need the shape of the lot. A rough diagram with side lengths marked can be photographed and uploaded to this site through the tools box.

Answer 1

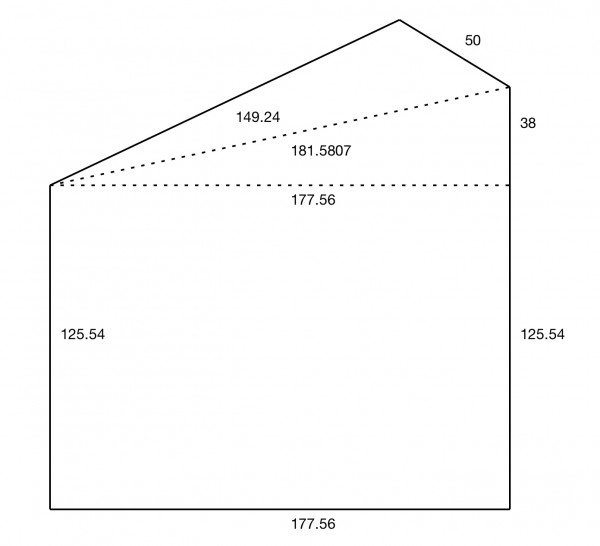
Your lot may not look like this but it has the dimensions you provided. Nevertheless, it may give you a guide on calculating the true area for yourself. The side 163.54 ft is split into two lengths 125.54+38=163.54.

The most difficult triangle to find the area of is right at the top. We use Pythagoras’ Theorem and the Cosine Rule to find more information. The hypotenuse of the right triangle near the top has length √(177.56²+38²)=√32971.55=181.58 ft approx.

The Cosine Rule gives us the highest vertex angle. 32971.55=149.24²+50²-2(149.24)(50)cosθ where θ is the angle. From this cosθ=(149.24²+50²-32971.55)/14924=-0.5494, and θ=123.32°. We use the formula ½absinθ to find the area of the top triangle=½(149.24)(50)sin123.32=3117.52 sq ft.

Now we add the areas of the rectangle and right triangle=

(125.54)(177.56)+19(177.56)+3117.52=28782 sq ft approx. The acreage is 28782/43560=0.66 acre.

Comments

Rod, thank you for the information.  The lot is actually an irregular pentagon.  I divided it into triangles and found an answer very similar to yours.  I was only wondering as I have been given several different answers. A landscape architect was the one who gave me the total closest to yours and mine. I think I will go with that. When a person sells their house it sounds much to be close to 7/10 of an acre than almost 1/2 of an acre. ( :

---

Hi Nancy. To find the area of an irregular pentagon, you can split it into just 3 triangles by choosing one vertex. This vertex is already connected to two others, so you only need to measure the distance to the remaining two vertices. You have the sides of the three triangles and now you have all you need to find their areas and hence the area of the pentagon. But then you probably knew that—and so did your architect!

---

Hello Rod!  And I talk to people all the time who say they never use the math skills and lessons from school!!  Thanks for the answer and a virtual pat on the back you probably didn't even know you shared!!  Smiles, Nancy