x²+y=37, x+y²=149,
So, subtracting the first equation from the second:
x+y²-x²-y=112,
y²-x²-(y-x)=112=(y-x)(y+x)-(y-x)=112
So (y-x)(y+x-1)=112
The factors of 112 can be grouped in pairs:
(1,112), (2,56), (4,28), (7,16), (8,14).
Let’s assume there is at least one integer solution for x and y, then we can find simultaneous equations using these factors.
Take the general case where the factors are a and b, so the 5 pairs above are examples of (a,b) and the simultaneous equations are:
y-x=a and y+x-1=b.
If we add these two equations we get:
2y-1=a+b, y=(a+b+1)/2, x=y-a.
If x and y are integers, we can eliminate those factors where a and b are both odd or both even. Also, since x²+y=37, x=√(37-y), y must be less than 37.
That leaves us with:
(1,112), (7,16)
a b x y x²+y y²+x
1 112 eliminate, because y=57>37
7 16 5 12 37 149,
so we have one integer solution (5,12).
However, there may be other solutions.
Since y=37-x² we can substitute for y in the second equation:
x+(37-x²)²=149,
x+1369-74x²+x⁴-149=0,
x⁴-74x²+x+1220=0.
We already know that x=5 is a solution so we can use synthetic division to reduce the quartic:
5 | 1 0 -74 1 | 1220
1 5 25 -245 |-1220
1 5 -49 -244
So x³+5x²-49x-244=0 is a cubic to be solved.
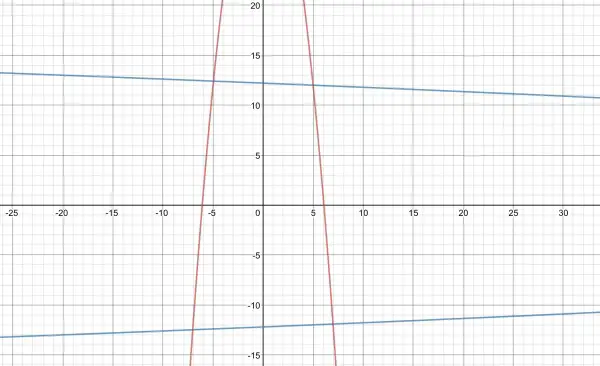
This shows the original equations graphically intersecting at four points. One of them is (5,12) as expected. To find the other three we can use the graph and Newton’s Method.
From the graph we can see the approximate x values at x=-5, -7 and 7.
To use Newton’s method we differentiate the cubic:
3x²+10x-49 and use the following iterative function:
x=x-(x³+5x²-49x-244)/(3x²+10x-49).
We start the process by setting x to one of -5, -7, 7 in the right hand expression, and we get a new value for x on the left hand side. This value is then plugged into the right hand expression to give another value for x on the left hand side, and so on. This will quickly give us each of the three solutions in the cubic for x, and we can use either of the two original equations to find y.
Using a calculator, I found 3 more pairs of values for (x,y) in addition to (5,12):
(-4.959029865,12.4080228),
(-7.035012262,-12.49139753),
(6.994042127,-11.91662527).