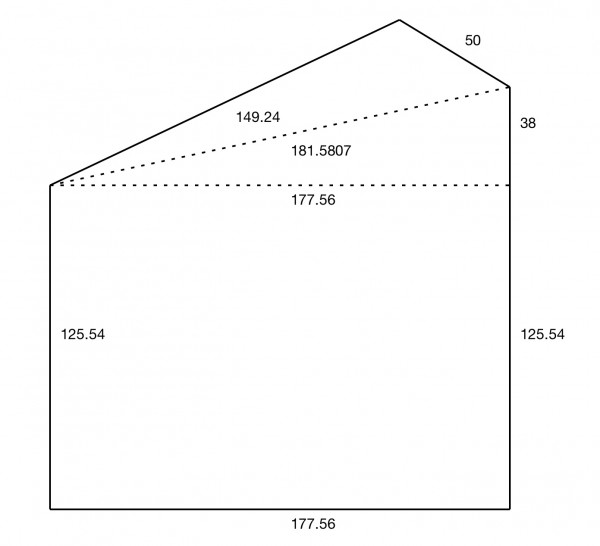
Your lot may not look like this but it has the dimensions you provided. Nevertheless, it may give you a guide on calculating the true area for yourself. The side 163.54 ft is split into two lengths 125.54+38=163.54.
The most difficult triangle to find the area of is right at the top. We use Pythagoras’ Theorem and the Cosine Rule to find more information. The hypotenuse of the right triangle near the top has length √(177.56²+38²)=√32971.55=181.58 ft approx.
The Cosine Rule gives us the highest vertex angle. 32971.55=149.24²+50²-2(149.24)(50)cosθ where θ is the angle. From this cosθ=(149.24²+50²-32971.55)/14924=-0.5494, and θ=123.32°. We use the formula ½absinθ to find the area of the top triangle=½(149.24)(50)sin123.32=3117.52 sq ft.
Now we add the areas of the rectangle and right triangle=
(125.54)(177.56)+19(177.56)+3117.52=28782 sq ft approx. The acreage is 28782/43560=0.66 acre.