Assume we can write 1/(y+3)=a(x+b) where a and b are constants. Plug in the given points:
(2,-2): 1=a(2+b) and (3,1): ¼=a(3+b). Divide these two equations to remove a:
4=(2+b)/(3+b), 12+4b=2+b, 3b=-10, b=-10/3.
Substitute for b: 1=a(2-10/3)=-4a/3, a=-¾. Therefore 1/(y+3)=-¾(x-10/3).
So inverting both sides: y+3=1/(-¾x+10/4)=4/(10-3x), and y=4/(10-3x)-3, y=(4-30+9x)/(10-3x).
Therefore y=(9x-26)/(10-3x) has an asymptote at y=-3 and passes through (3,1) and (2,-2). It also has an asymptote at x=10/3.
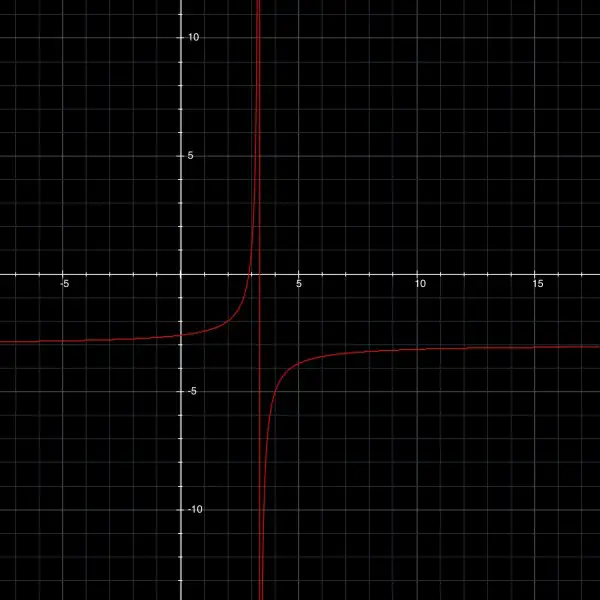
Note the graph has two parts and the asymptotes are common to both parts at y=-3 and x=3⅓. The left component is similar to the graph submitted in the question. The vertical asymptote is shown on the graph above but it is not part of the graph itself.