4. Find the question of the normal line to the curve described by the equation y=x4-3x2+2x at the point x=2

Question

1.Find the question of the normal line to the curve described by the equation y=x4-3x2+2x at the point x=2

2. Find the diameter and height of a cylinder of maximum volume which can be cut from a sphere of radius 12 cm  .

Answer 1

1. To find the equation of the normal when x=2, first differentiate y:

dy/dx=4x³-6x+2. This is the gradient of the tangent. When x=2 dy/dx=32-12+2=22, so the gradient of the normal is -1/22. y(2)=16-12+4=8, so the normal is at point (2,8).

The equation of the normal is y-8=-(x-2)/22, y=-x/22+1/11+8=-x/22+89/11.

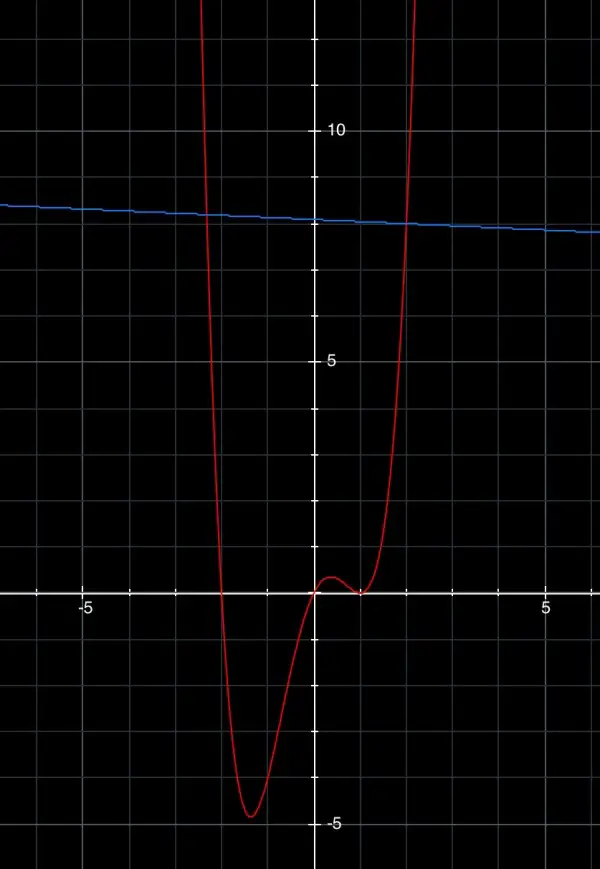
The blue line is normal to the red curve at (2,8).

2.

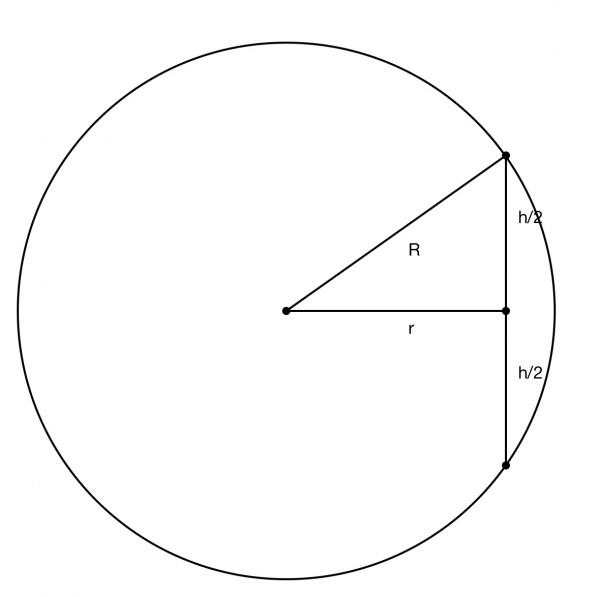
The height h, radius r of the cylinder, and radius R of the sphere are related by Pythagoras’ Theorem.

R²=(½h)²+r². Since R=12cm, h=2√(144-r²) and volume of the cylinder V=πr²h=2πr²√(144-r²).

The rate of change of volume with respect to the radius is dV/dr:

dV/dr=-2πr³/√(144-r²)+4πr√(144-r²)=0 at extrema.

So -2πr³+4πr(144-r²)=0, and r=0 (minimum volume) and -r²+2(144-r²)=0, r=√96=4√6 cm (maximum volume).

h=2√(144-96)=8√3 cm. So the diameter is 2r=8√6=19.60 cm and h=13.86 cm approx.