Let the husband and wife couples be:
Alan and Alice
Barry and Barbara
Charles and Charlotte
David and Diane
Possible 12 teams are:
- Alan and Barbara
- Alan and Charlotte
- Alan and Diane
- Barry and Alice
- Barry and Charlotte
- Barry and Diane
- Charles and Alice
- Charles and Barbara
- Charles and Diane
- David and Alice
- David and Barbara
- David and Charlotte.
Now we create opposing teams by selecting a team, say team 1. Then we eliminate all teams containing the same players, that is, all teams containing Alan or Barbara. That eliminates teams 2, 3, 8, 11, leaving 7 eligible teams as opponents. Each team, in fact, will have 7 eligible opposing teams and there are 12 teams, so there can be 12×7=84 games. But, wait a minute! Let’s take just one game, say team 1 against team 7. When we get to looking at the games team 7 can play we will include team 7 against team 1. Unless, the position of the players in the tennis court is relevant, team 1 against team 7 is the same as team 7 against team 1. So we have to halve the number of games, making it 84/2=42 games.
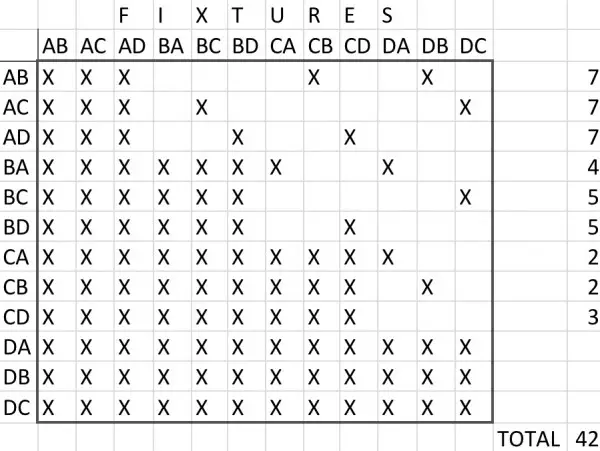
The fixtures are shown above. X means there can be no game. The blank cells represent valid games, 42 in all.