A sheep pen

Question

a farmer wishes to build a rectangular sheep pen with 200m fence, using one side of an existing shade as the side. the shed is also rectangular of measurement 30m x 30m. a) find the measurement and the area of the sheep pen if the one side of the existing shed is used as the width of the sheep pen. b) by using the fence of the same length and using the width of the shed as part of the width of the sheep pen, find the length and the width of the sheep pen with maximum c)if two sheep pens of the same size are built adjacent to each other, find i)the length of the new sheep pen if one side of the shed is used as the width of the sheep pen ii)the length and the width of the sheep pen, which is adjusted so that the enclosed area is maximum d)find the maximum enclosed area if the same fence is used to construct three rectangular sheep pens.

Answer 1

This answer has now been revised. I hope it's correct according to the given figures. Sorry for the error. I must have confused two very similar questions.

The perimeter of the pen is 2L+2W where L and W are length and width.

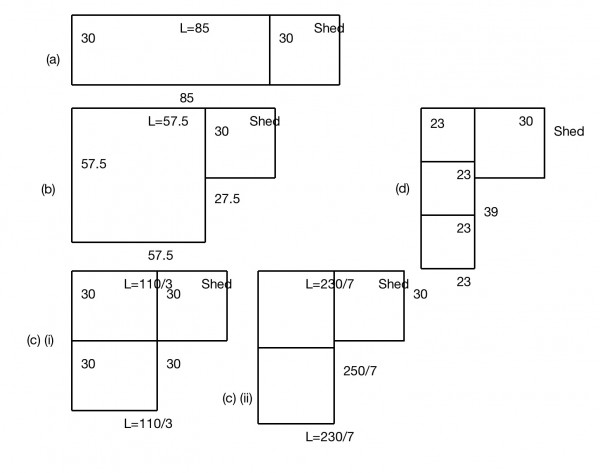
(a) The fence has a length 2L+W because the shed's length is 30m and forms a width. Since W=30, 2L+30=200, 2L=170, L=85m. The area is 30*85=2550 sq m. [corrected]

(b) The maximum area for the pen is a square, so L=W and the area is L^2. The perimeter is 4L. We know that the shed helps to form a side. So the perimeter is 200+30=230m=4L, so L=57.5m and the area is 3306.25 sq m. [corrected] It's easy to prove that a square is the maximum area for a given perimeter. If L=a-x and W=a+x, the fixed perimeter, P,  is 4a, so a=P/4. The area is a^2-x^2. This quantity has a maximum value of a^2 only when x=0, which means L=W=a, a square.

(c) (i) Now, if the length of each pen is L and the total amount of fencing is 200m, then we can write an equation for the total amount of fencing:  3L+3W=200, where W=30, since the shed covers the width of one pen, so L=110/3=36 2/3m. (ii) If the two pens are square for maximum area each, and the side is L, the total enclosed perimeter is 7L. The perimeter is made up of 200m of fence and 30m of shed=230m. L=230/7=32 6/7m=32.857m approx. [corrected]

(d) For three pens of maximum area the perimeter is 10L=200+30=230, and L=23m. The area of each pen is 529 sq m. [corrected] Total pen area is 1587 sq m.

Comments

Sis and Nur: I have revised my answer following your corrective comment. I hope the answer makes sense.

---

I've deleted the other question as you requested.