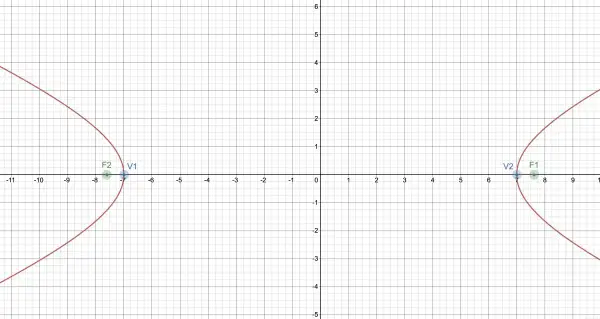
Vertices, centre and foci lie on the same line. The y-coordinates of the given vertices and foci are the same, that is, y=0. This means that the centre of the hyperbola also lies on y=0, the x-axis.
The vertices are at (7,0) and (-7,0) and the centre of the hyperbola is midway between these two points, so the centre of the hyperbola is at the origin (0,0).
The general equation of a horizontal hyperbola is (x-h)2/a2-(y-k)2/b2=1, where a is the distance between the centre and each vertex. Therefore a=7. (h,k)=(0,0), being the centre. We have to find b. The distance from the centre to each focus is given by c=√(a2+b2). We know the foci are at (√58,0) and (-√58), so c=√58 making a2+b2=58, so b2=58-a2=58-49=9, and b=3. The equation of the hyperbola is:
x2/49-y2/9=1