(3) The equation can be written:
9x²-36x+16y²+96y+36=0,
9(x²-4x+4)+16(y²+6y+9)+36-36-144=0,
9(x-2)²+16(y+3)²=144,
(x-2)²/16+(y+3)²/9=1⇒centre is at (2,-3). Semimajor axis, a=√16=4, semiminor axis, b=√9=3.
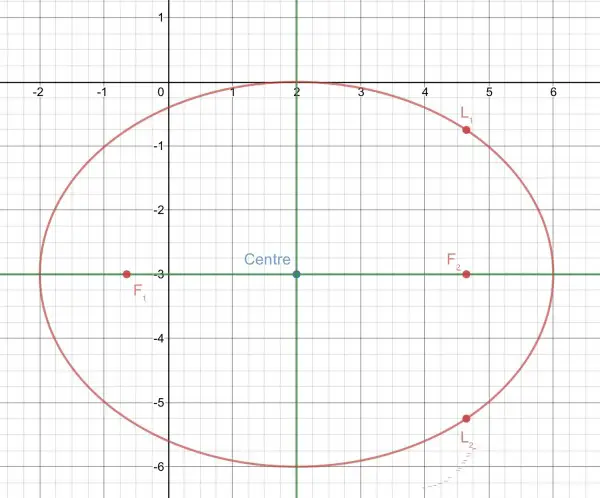
The axes of the ellipse are shown in green.
Focal distance from the centre is √(a²-b²)=√(16-9)=√7.
Foci are (2-√7,-3) and (2+√7,-3) because the foci lie on the major axis (y=-3).
Eccentricity, e²=(1-(b/a)²)=1-9/16=7/16, e=√7/4.
Latus rectum is a chord that passes through a focus, is perpendicular to the major axis and meets the curve (at both ends). F₂ (see graph) lies on the line x=2+√7, so it meets the ellipse at 7/16+(y+3)²/9=1. y+3=±√(81/16)=±9/4, so the length of the LR is 9/4-(-9/4)=9/2. L₁ is (2+√7,-3+9/4)=(2+√7,-¾) and L₂ is (2+√7,-3-9/4)=(2+√7,-21/4).
(4) No information about hyperbolas supplied.