The basic expression for the integrand is 2πyds, where y=f(x) and ds is an infinitesimal segment of the curve. ds is related to dy and dx by ds²=dy²+dx², so (ds/dx)²=(dy/dx)²+1 and ds=√((dy/dx)²+1). The surface area A=2πʃyds=2πʃy√((dy/dx)²+1)dx.
If y=-1/√(3x+1)=-(3x+1)^-½ then dy/dx=3/(2(3x+1)^(3/2)), (dy/dx)²=9/(4(3x+1)³), and √((dy/dx)²+1=√((9+4(3x+1)³)/(4(3x+1)³)).
A=2πʃ(-1/√(3x+1))√((9+4(3x+1)³)/(4(3x+1)³))dx,
A=-πʃ[√(9+4(3x+1)³)/(3x+1)²]dx.
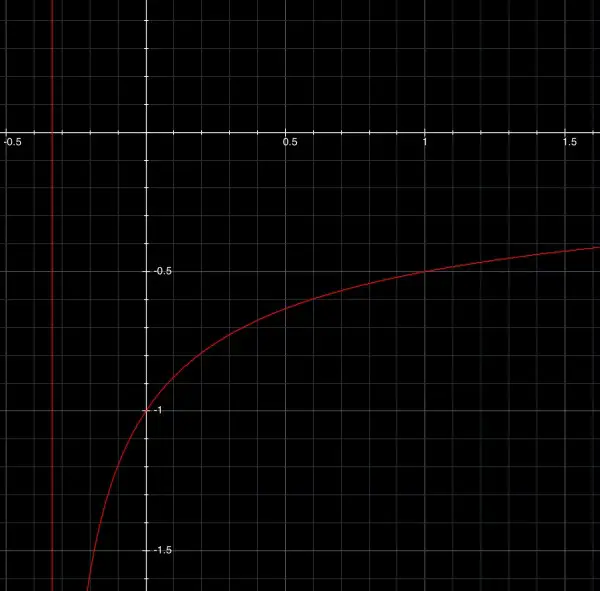
f(x) has a vertical asymptote at x=-⅓ and the x-axis is a horizontal asymptote. The limits for the integral are therefore -⅓≤x≤∞ if the whole curve is to be rotated around the x-axis. At x→-⅓, the integrand approaches infinity, so the surface area is infinite. Below f(x) is shown as the red curve and the asymptote as a vertical red line.