what is the area of 20ft, 7ft, 21ft, 30ft

Question

I need to explain to my daughter how to find the area and I'm not sure how to do that.  The question is:

What is the area of the figure below?  The dimensions are 20ft, 7ft, 21ft, 30ft

Answer 1

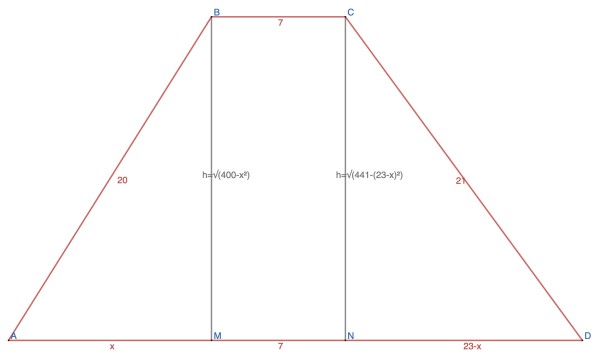
Unfortunately, there's no diagram, so I'm going to guess what shape we have here.

Since four dimensions have been given and they're all different, I guess we have a quadrilateral we could call ABCD where the side lengths are in cyclic order: AB=20', BC=7', CD=21', DA=30'. Let's assume we have trapezoid in which BC is parallel to AD.

To find the area A=½(b₁+b₂)h where b₁ and b₂ are the lengths of the parallel sides and h is the height. We need to find h. Drop a perpendicular BM from B on to AD and another CN from C to AD. BM=CN=h feet.

By Pythagoras, BM²=AB²-AM²=h²=CD²-ND². AM+MN+ND=30. But MN=BC=7. Let x=AM, then ND=30-7-x=23-x.

So h²=20²-x²=21²-(23-x)². 

20²-x²=21²-(23-x)²,

20²-x²=21²-23²+46x-x²,

400=441-529+46x,

46x=529+400-441=488, x=488/46=244/23.

Therefore h=√(20²-(244/23)²)=16.9545' (approx).

b₁=BC=7', b₂=DA=30', A=½(37)(16.9545)=313.66 sq ft approx.

This is the area of a trapezoid (as defined above) and may not be the actual shape you intended.