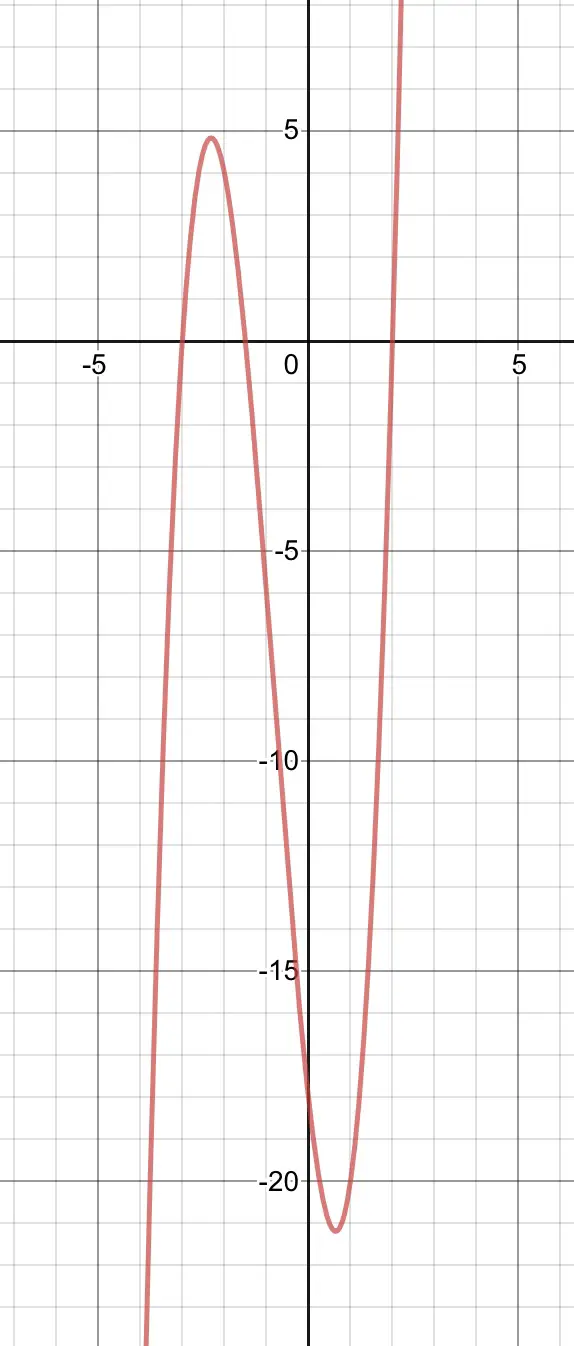
f(x)=(2x+3)(x+3)(x-2)=2x³+5x²-9x-18.
Using the Rational Zeroes Theorem, we find all the factors of 18=1, 2, 3, 6, 9, 18. And all the factors of 2=1, 2.
We need to find the coefficients of x and the constants such that:
(ax+b)(cx+d)(ex+f), such that ace=2, bdf=-18. If a=2, then c=e=1. So we know that if we have rational factors the factorisation will be (2x+b)(x+d)(x+f). We take each factor with plus and minus and find out which, if any, make f(x)=0. These are the values we have to plug in till we get zero:
1, -1, 2, -2, 3, -3, 6, -6, 9, -9, 18, -18.
Start with x=1: 2+5-9-18=-20, x=-1: -2+5+9-18=-6, x=2: 16+20-18-18=0. So x=2 is a zero.
Use synthetic division to divide by this zero and get a quadratic:
2 | 2 5 -9 -18
2 4 18 18
2 9 9 0 = 2x²+9x+9=(2x+3)(x+3).
So we now know f(x)=(x-2)(2x+3)(x+3), zeroes are 2, -3/2, -3 which are the x-intercepts of the graph of the cubic. The y-intercept is the constant term -18.