Find two level curves of the function � ( � , � ) = 25 − � 2 − � 2 g(x,y)= 25−x 2 −y 2 ​ .

Question

this question is relate to level curve steward 9th edition caluculas

Answer 1

This question is a little confusing to interpret. This is my interpretation.

g(x,y)=25-x²-y² is a 3-dimensional curve. It can be shown that it's a hollow paraboloid, and any horizontal cross-section will be a circle. This is what the level curve gives us for different horizontal planes slicing across the paraboloid. A paraboloid is like a cone with curved sides. Its vertical cross-sections are parabolas.

Let z=g(x,y), then z=25-x²-y², so x²+y²=25-z. This is the equation of a circle where radius r is √(25-z).

When z=25, x²+y²=0. The only real solution to this equation is x=y=0, that is, the origin (0,0), representing the apex of the paraboloid in the horizontal x-y plane at a vertical position of z=25 (25 units above the 3-space origin (0,0,0)).

When z=0, x²+y²=25, which is a circle of radius 5 and centre at the origin. If z>25 there are no real solutions for x and y, so when z=0, we have the x-y plane intersection with the paraboloid. So the set of level curves is an infinite set of concentric circles which, if stacked on one another would create the outer surface of a paraboloid of infinite height.

If z<0, for example, z=-144, x²+y²=169=13², we have a circle radius 13, centre at the origin. The paraboloid has no definite base, because as z becomes more negative the paraboloid widens indefinitely. However, its apex (highest point) is fixed at (0,0,25) in 3-space.

 

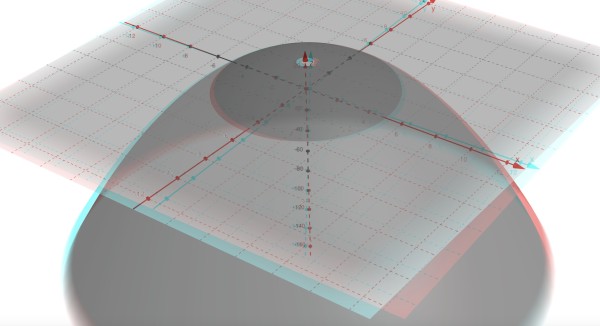
The image is best viewed using 3D glasses (left eye red, right eye green or blue).